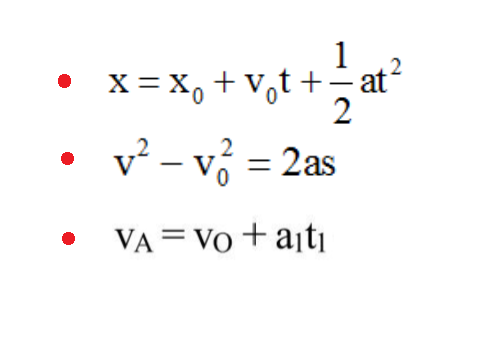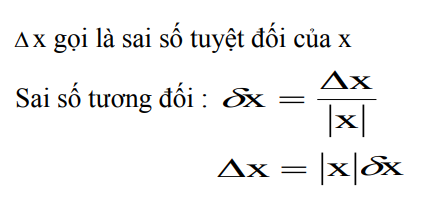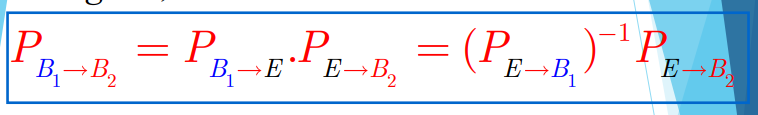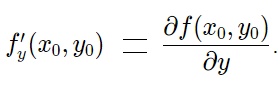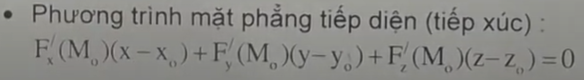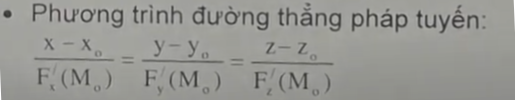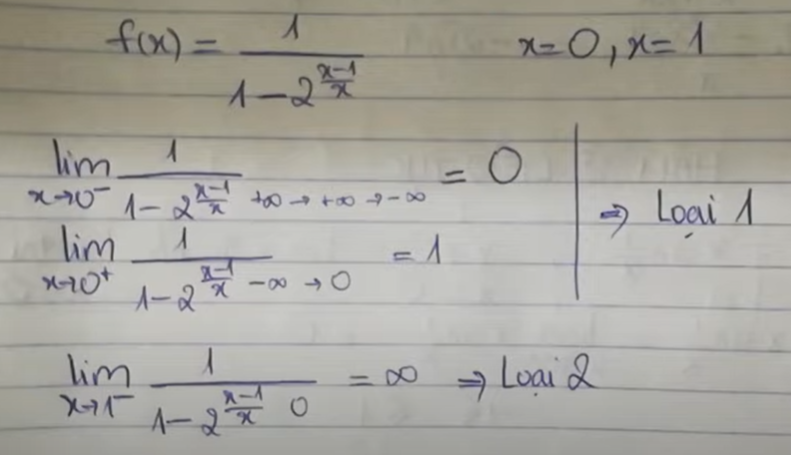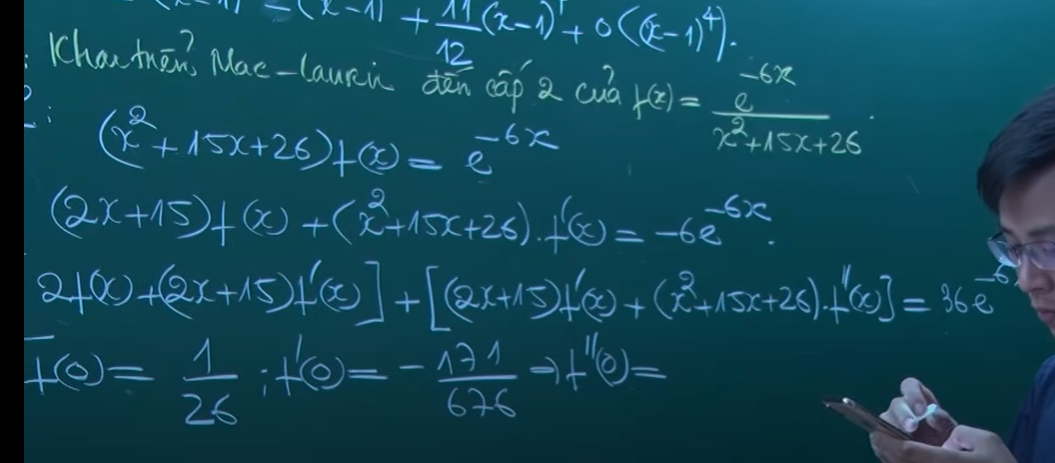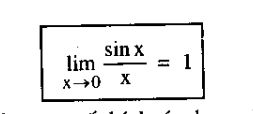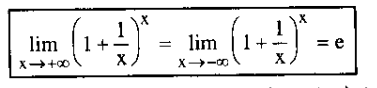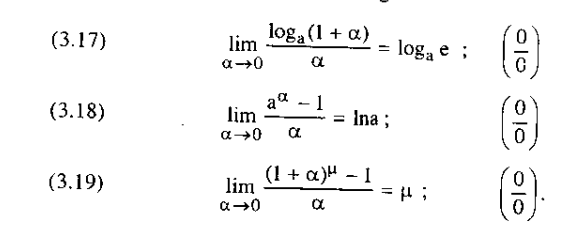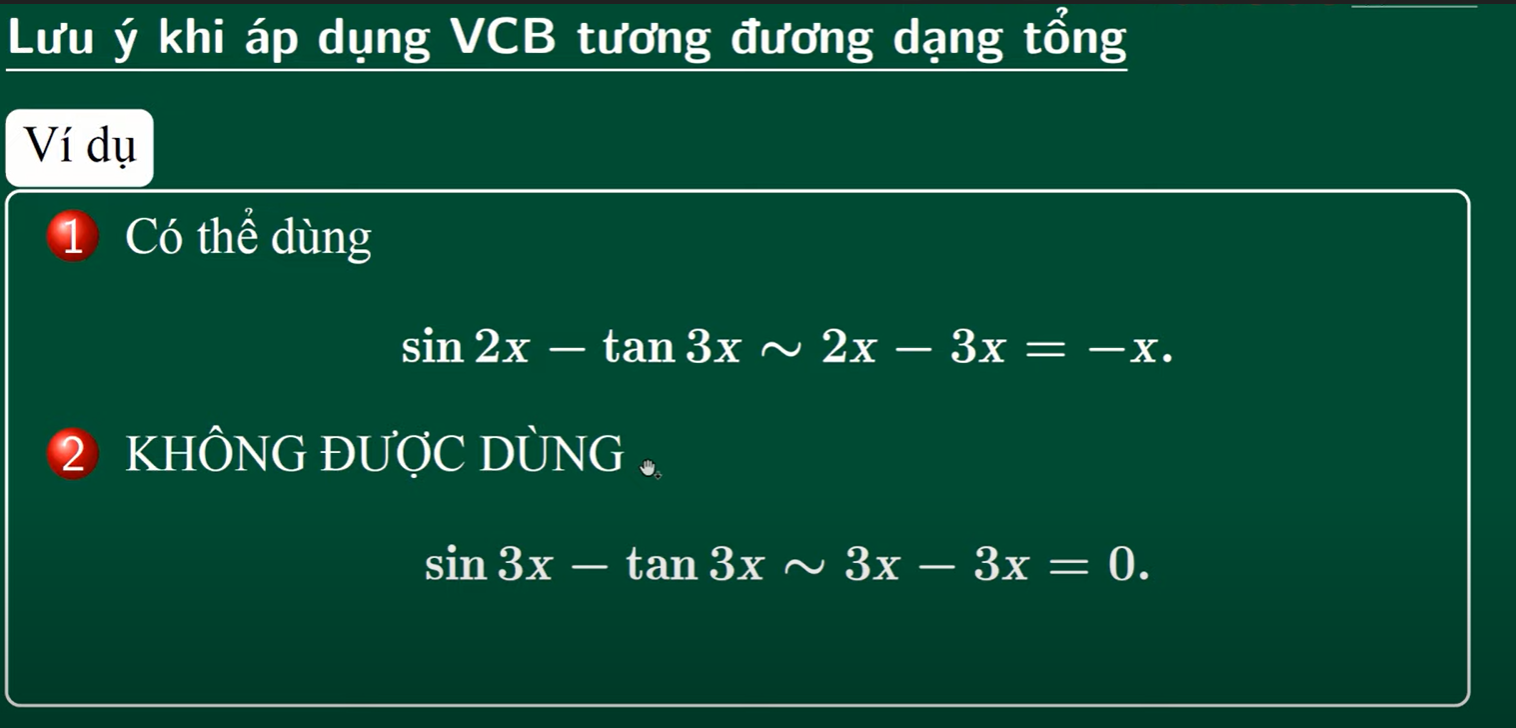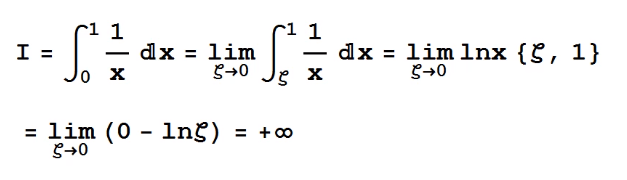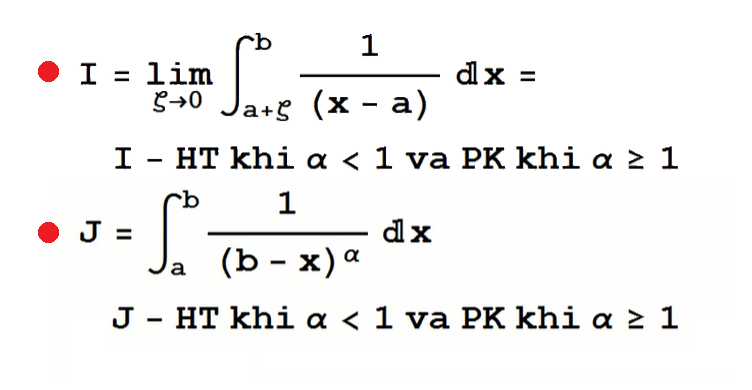Last updated：October 3rd 2022, 20:34

Year 1: Semester 2

Thi Cuối kỳ:

P.Pháp Tính:
Lý:
Toán rời rạc:
C.trúc dữ liệu:
C.trúc máy tính & vi xử lí:
- Tổng quan: 60 phút thi, 30 câu TN + 2 TL
- 6 điểm: 30 câu trắc nghiệm: trải dài 7 chương
- 4 điểm: 2->3 câu tự luận: tập trung chương 1:
  - Câu 1: cpi,hiệu năng, chu kì, mibs, speed up
  - Câu 2: liên quan bộ nhớ, chip nhớ, tương tự bài trong giữa kì 2
  - câu 3: bộ nhớ cache
    - bài tập tìm bit của từng line như hồi ktra giữa kì 2
    - tính tỉ lệ hit, miss
    - tính thời gian truy cập trung bình

Conclusion Endterm

Phương pháp tính

C.trúc dữ liệu

Đề cương:

Nội dung
Đề mẫu
Đề Năm Ngoái

Toán rời rạc

Đề cương
Đề mẫu của thầy Tao
Giải
Đề năm ngoái

C.trúc máy tính và VXL

Đề ôn 21clc-1:
Trang 1
Trang 2
Trang 3
Trang 4
Tổng hợp cả 4 trang

Tự luận
Đáp án

Tóm tắt cách chuyển binary sang IEEE 754
- số đầu là dấu (1 = âm)
- chuyển 8 số sau sang dec = e
- 8 số tiếp theo sang dec = m
- đáp án = (dấu) 1(phẩy)m * 2^(e-127)

Vật lý 1

Nội dung thi giữa kì:

Sách bài tập VL1: [pdf]
Lời giải: link

Chương 6 Điện trường:

Bài 2
Bài 4 (thiếu câu d)
Bài 7 (thiếu câu b)

Chương 9 Từ trường:

Bài 1
Bài 2
Bài 4
Bài 6
Bài 8

Chương 10 Cảm ứng điện từ:

Bài 4
Bài 5
Bài 6
Bài 8
Bài 10

Conclusion Midterm

Phương pháp tính

C.trúc dữ liệu

Dàn ý Code
Code giao diện
Code nhập data, in, tìm kiếm

Toán rời rạc

Chú ý đọc đề, đổi số liệu
A = P = Chỉnh hợp, C = tổ hợp
Câu 1
Câu 2
Câu 3
Câu 4

C.trúc máy tính và VXL

Câu 1: Biến đổi - cộng hexa

Web hỗ trợ chuyển đổi
- Biến đổi thập,nhị phân sang thập lục phân: rapidtables.com
- Cộng trừ hex www.calculator.net
Lời giải

Câu 2:

Web chuyển đổi dạng IEEE 754-32 về thập phân và ngược lại
- theza2.mobie.in
Chuẩn IEEE 754-32 về thập phân
- IEEE 754-32: S (1)|E (8)|M (23)
- IEEE 754-8: S (1)|E (3)|M (4)

Câu 3:

Cache liên kết kiểu tập hợp - Set Associative Caches
Two-way Set Associative Caches
Ảnh hưởng đến bit nào của thanh ghi cờ

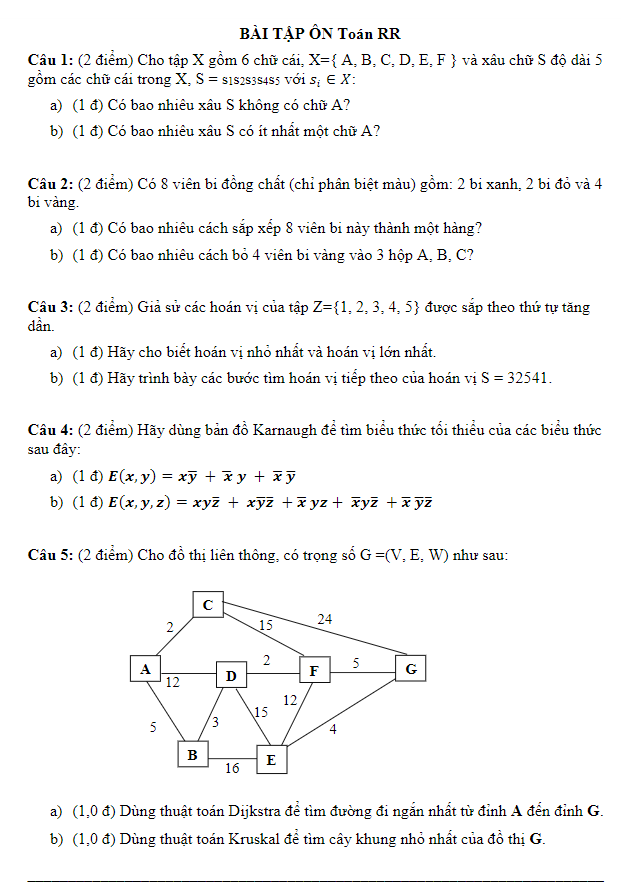
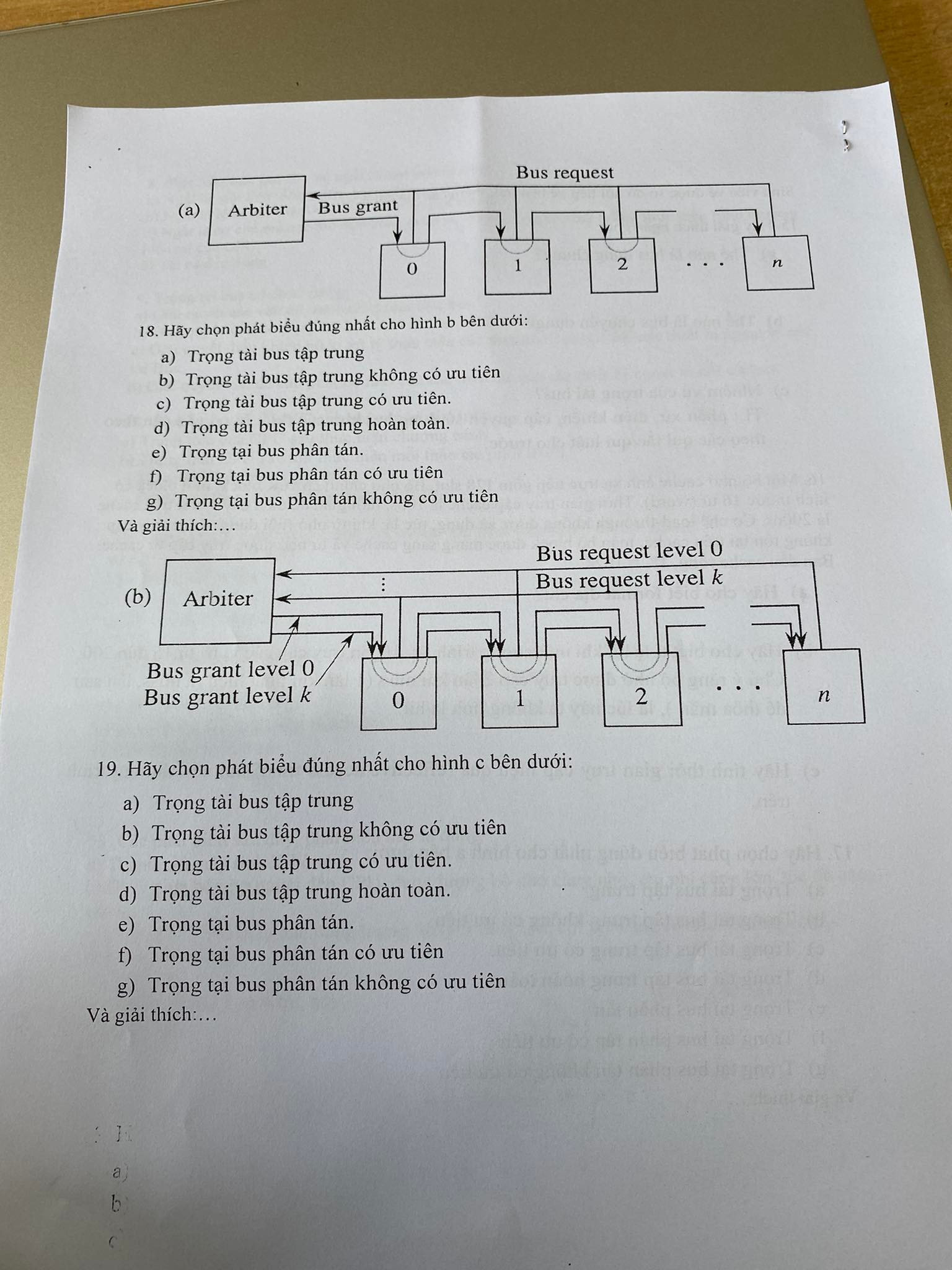
Câu 4:

Giải mã hình ảnh
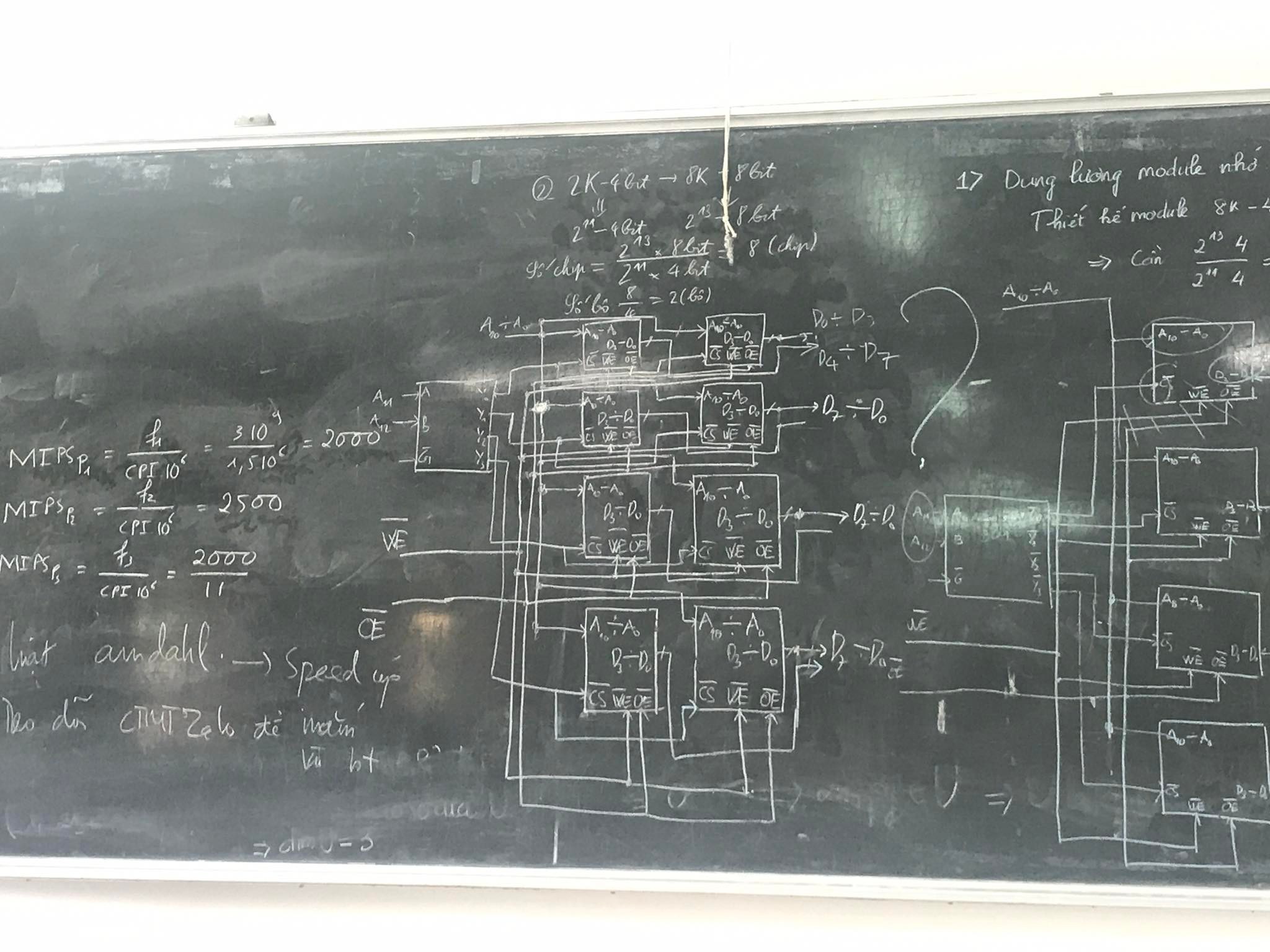
Vẽ hình thiết kế modun nhớ

Cũ rồi
- CPU Execution Time, CPI, MIPS:

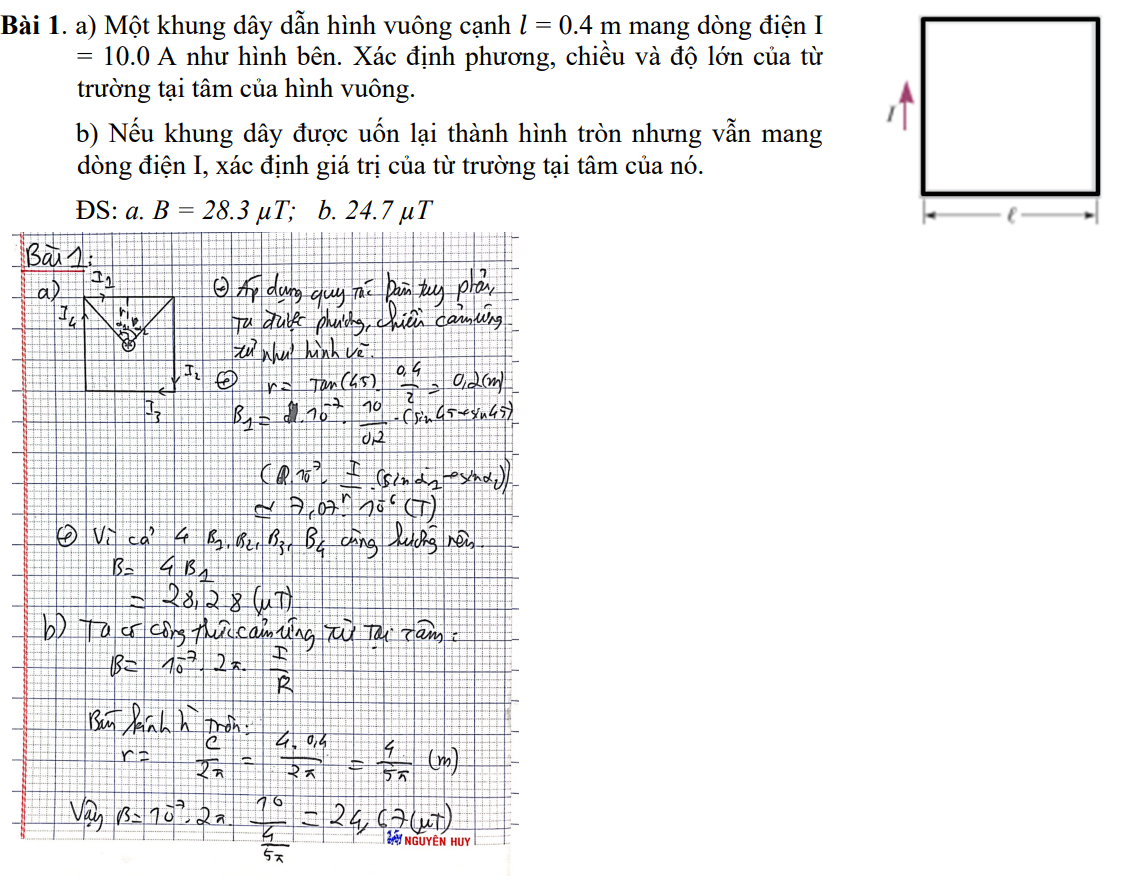
Vật lý 1

Nội dung thi giữa kì: [pdf]

Sách bài tập VL1: [pdf]
Lời giải cho sách bài tập: [link]

Dùng chung (chưa rõ):

3 công thức cđ nhanh dần đều

Câu 1 (1đ, Lý thuyết):

Lý thuyết
- Sup

Câu 2 (dự đoán Chương 2: ĐLHọc Chất Điểm):

Định luật 2 Newton và Công thức nhanh/chậm dần đều
- Cách làm:
  - Bước 1: Đặt trục Ox,Oy, Phang công thức Đl2 newton
  - Bước 2: Xét phương trình trên trục Oy, thường sẽ tìm được N. Xét trên Ox sẽ được p.trình nào đóng
  - Bước 3 (Optional): Nếu chưa giải ra, thì kết hợp c.thức nhanh dần đều

Câu 3 (dự đoán Chương 3: ĐLHọc Vật rắn (Hệ chất điểm)):

Bài 2
Bài 3
Bài 5

Câu 4 (dự đoán Chương 3):

Bài 7
Bài 8
Bài 9

Câu 5 (dự đoán Chương 4: Công và Cơ năng):

Tên bài
- sicko mode

Note Books Sem2-Year1

Phương pháp tính

Tổng quan chương trình

Quá trình dạy học: [pdf]
Mục lục: Giáo trình [pdf]
- Học đến hết chương 4
- Thi giữa kì
- Từ chương 4 đến hết chương 8
- Thi cuối kì

Giữa kì

Chương 2: Tổng hợp kiến thức sai số:

Liên hệ giữa sai số tuyệt đối & tương đối
Ví dụ sai số của Hàm số

Chương 3: Tính giá trị hàm:

Sơ đồ hoocner và thuật toán
Sơ đồ hoocner Tổng Quát và thuật toán

Chương 4: Giải gần đúng phương trình:

Để tìm nghiệm gần đúng, ta có 2 cách:
Tách nghiệm:
- Phương pháp đồ thị
- Định lí 1 và ví dụ
- Định lí 2 (tìm sai số tuyệt đối) và ví dụ
- Định lí 3 và ví dụ
- Định lí 4 và ví dụ
Chính xác hoá nghiệm: 4 phương pháp
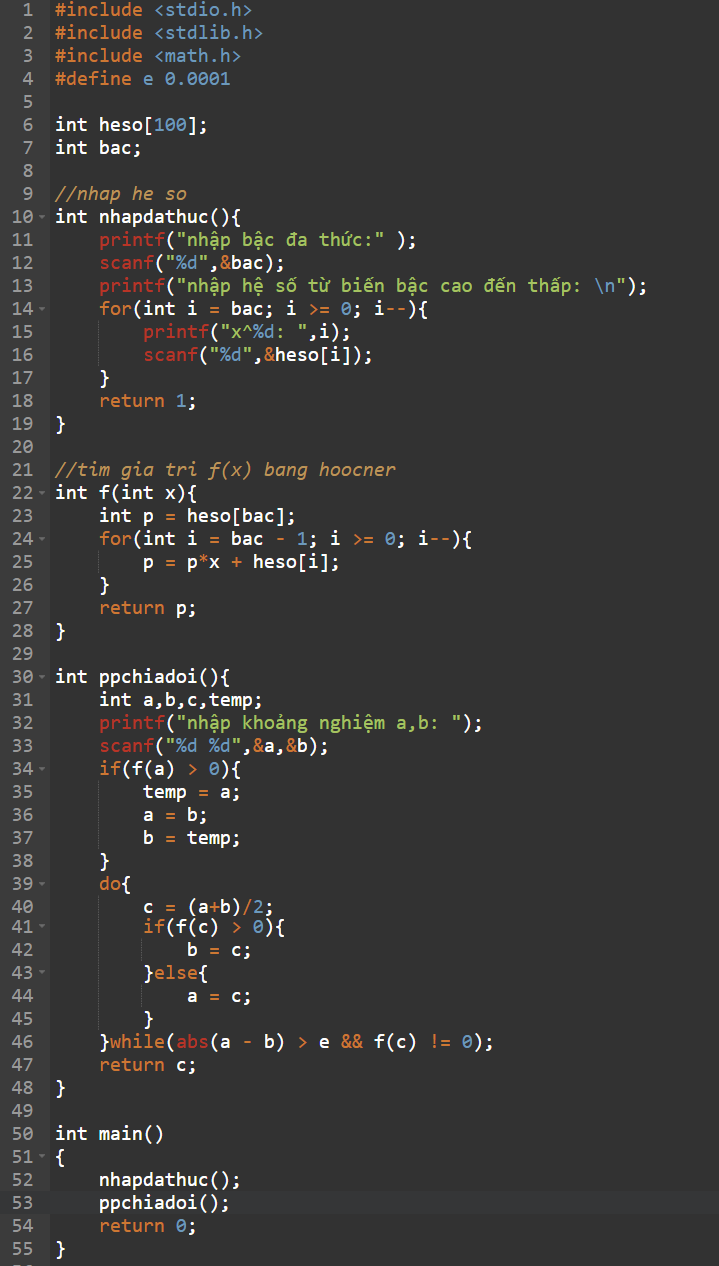
- Phương pháp chia đôi
  - Giải thích:
  - Thuật toán:
  - Code:
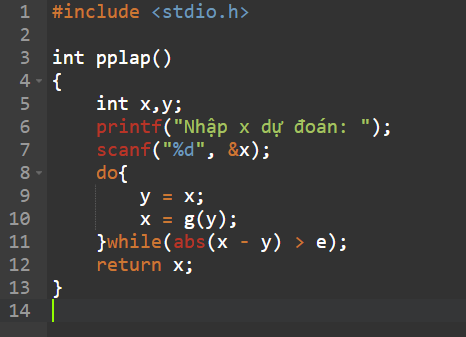
- Phương pháp lặp
  - Cách tìm g(x):
  - Tìm được g(x) rồi thì viết code như ppchia đôi
- Phương pháp tiếp tuyến
  - Thuật toán:
- Phương pháp dây cung
  - Thuật toán:

Cuối kì

Chương 5: Giải hệ p.trình đstt:
- PP Krame:
  - only code
- PP Gauss:
  - Biến đổi thành tam giác trên rồi giải nghiệm
- ❌PP Gauss - Siedel:
- ❌PP Giảm dư:
Chương 6: Tìm Gtrị riêng, vector riêng:
- ❌Tìm gtrị riêng bằng pp Đanhilepski
- ❌Tìm vector riêng bằng pp Đanhilepski
Chương 7: Nội suy và pp bình phương bé nhất:
- Tìm đa thức nội suy Lagrange (2 cách)
  - Cách 1 là đủ
- ❌Tìm đ.thức nội suy Lagrange với điểm nội suy cách đều
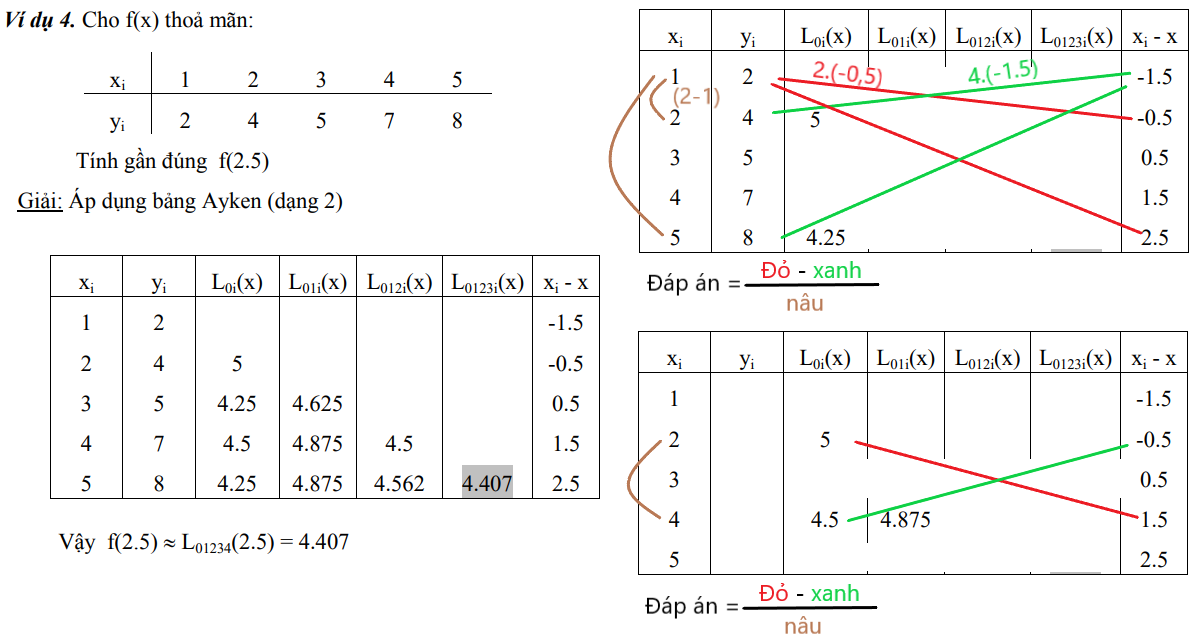
- Bảng nội suy Ayken (2 dạng)
  - Dạng 1: Đọc giáo trình đủ hiểu
  - Dạng 2:
    - Tóm tắt
- Nội suy Newton
  - Tóm tắt
- Nội suy Hecmit
  - Tóm tắt
- PP Bình phương bé nhất (có 3 dạng)
  - ❌Dạng y = a + bx
  - ❌Dạng y = a + bx + c.x^2
  - Dạng y = a.x^b hoặc y = a.e^bx:
    - Tóm tắt
Chương 8: Tính gần đúng tích phân xác định:
- Công thức hình thang
- Công thức parabol
- Công thức Newton-Cotet

C.trúc dữ liệu

Tổng quan chương trình

Quá trình dạy học: [xxx]
Mục lục: Giáo trình:[pdf]
- Thi giữa kì
- Thi cuối kì

Toán rời rạc

Tổng quan chương trình

Quá trình dạy học: [xxx]
Mục lục: Giáo trình:[pdf]
- Chương 1: [Bài toán đếm-tồn tại]
- Thi giữa kì
- Thi cuối kì
Đề giữa kì:
- ĐT clc kì2/2020 (Khóa 20): [pdf]

Soạn bài

Chương 1: Bài toán đếm-Bài toán tồn tại:
- Các nội dung trong chương 1:
  - Các nguyên lí cơ bản
    - Nguyên lí nhân: k cần quan tâm
    - Nguyên lí cộng: k cần quan tâm
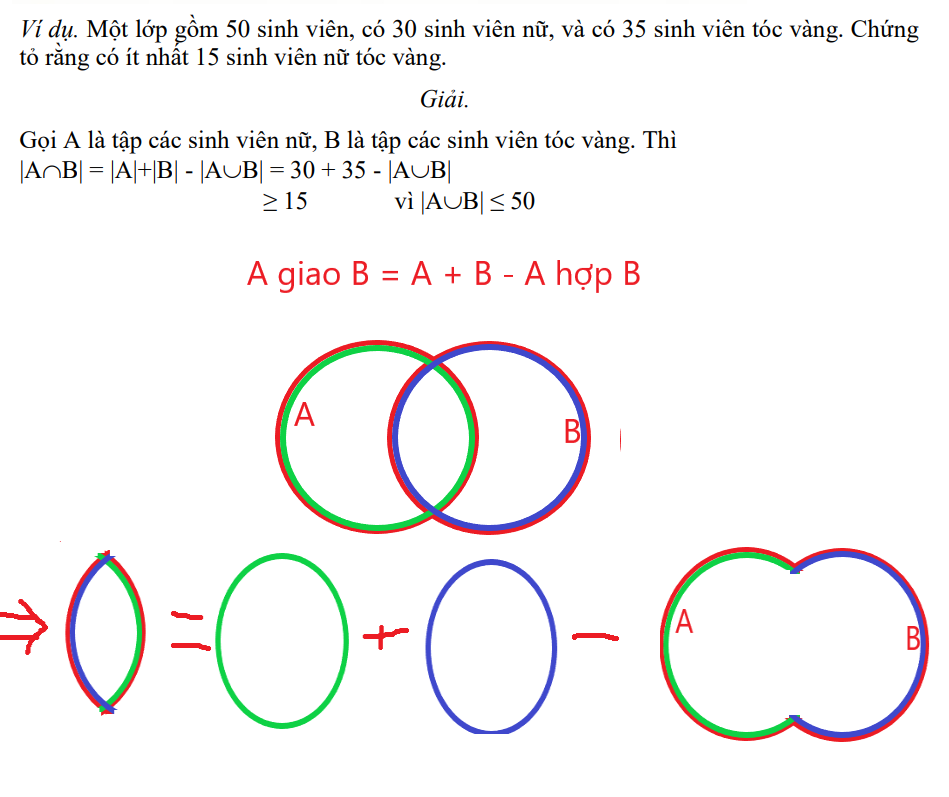
    - Nguyên lí bù trừ:
    - Nguyên lí Dirichlet: là bài toán nhốt thỏ vào lồng
  - Các cấu hình tổ hợp cơ bản
    - Chỉnh hợp lặp:
    - Chỉnh hợp:
      - Như cũ, có 4 con số từ 1->9, bóc 2 con để tạo số 2 chữ số => 4A2 = 4P2 = 12
    - Hoán vị
      - Như cũ, 1 hàng dài có 4 người, tìm các cách xếp => 4!
    - Tổ hợp
      - Như cũ, có 4 cây kẹo, bóc 2 cây => 4C2 = 6
    - Các công thức tổ hợp: ???
  - Các cấu hình tổ hợp suy rộng
    - Hoán vị lặp:
    - Tổ hợp lặp: Nguồn ytb: [https://youtu.be/BxV1bOJU4j8?t=89]
Chương 2: Kỹ thuật đếm nâng cao:
- Hệ thức truy hồi

C.trúc máy tính và VXL

Tổng quan chương trình

Quá trình dạy học: [pdf]
Mục lục:
- Chương 1: [GIỚI THIỆU CHUNG]
- Chương 2: [B.DIỄN D.LIỆU TRONG CÁC H.THỐNG M.TÍNH]
- Chương 3: [HỆ THỐNG MÁY TÍNH]
- Chương 4: [Memory System]
- Thi giữa kì: Từ chương 5 đến hết chương 7
- Chương 5: [HỆ THỐNG NHỚ]
- Chương 6: [VÀO – RA]
- Chương 7: [TỔ CHỨC XỬ LÝ SONG SONG]
- Thi cuối kì
Đề giữa kì:
- Nhật clc kì1/2021 đề 1: [pdf]
- Nhật clc kì1/2021 đề 2: [pdf]
- HCM I suppose: [Link]

Chương Input - Output

ko có gì hot

Chương Processor Structure & Function

Register (thanh ghi) là một bộ phận trong CPU (Processor)
- Trong CPU thì gồm nhiều nhóm register nhỏ
  - General register, … (xem ảnh)
Instruction Pipeling Pipelining Strategy

Giải ngố định nghĩa

Thông số máy tính
Tìm MIPS
- casc

Vật lý 1

Tổng quan chương trình

Quá trình dạy học: [pdf]
Mục lục:
- Cơ học: 5 chương [pdf]
- Thi giữa kì: vị trí dừng: hết chương 6
- Điện từ học: 5 chương [pdf]
- Thi cuối kì

Tự đọc

Chương 1:
- page 5: Hệ tọa độ đề các, hiểu nôm na là có vật M chuyển động theo 1 quỹ đạo, ta lấy 1 gốc bất kì là O, từ đó có vector OM. Ta có thể lấy tọa độ đề các trên không gian 2-3 chiều tùy bài
Chương 3:
- Giải thích khái niệm: [Khối tâm,Vị trí,…]
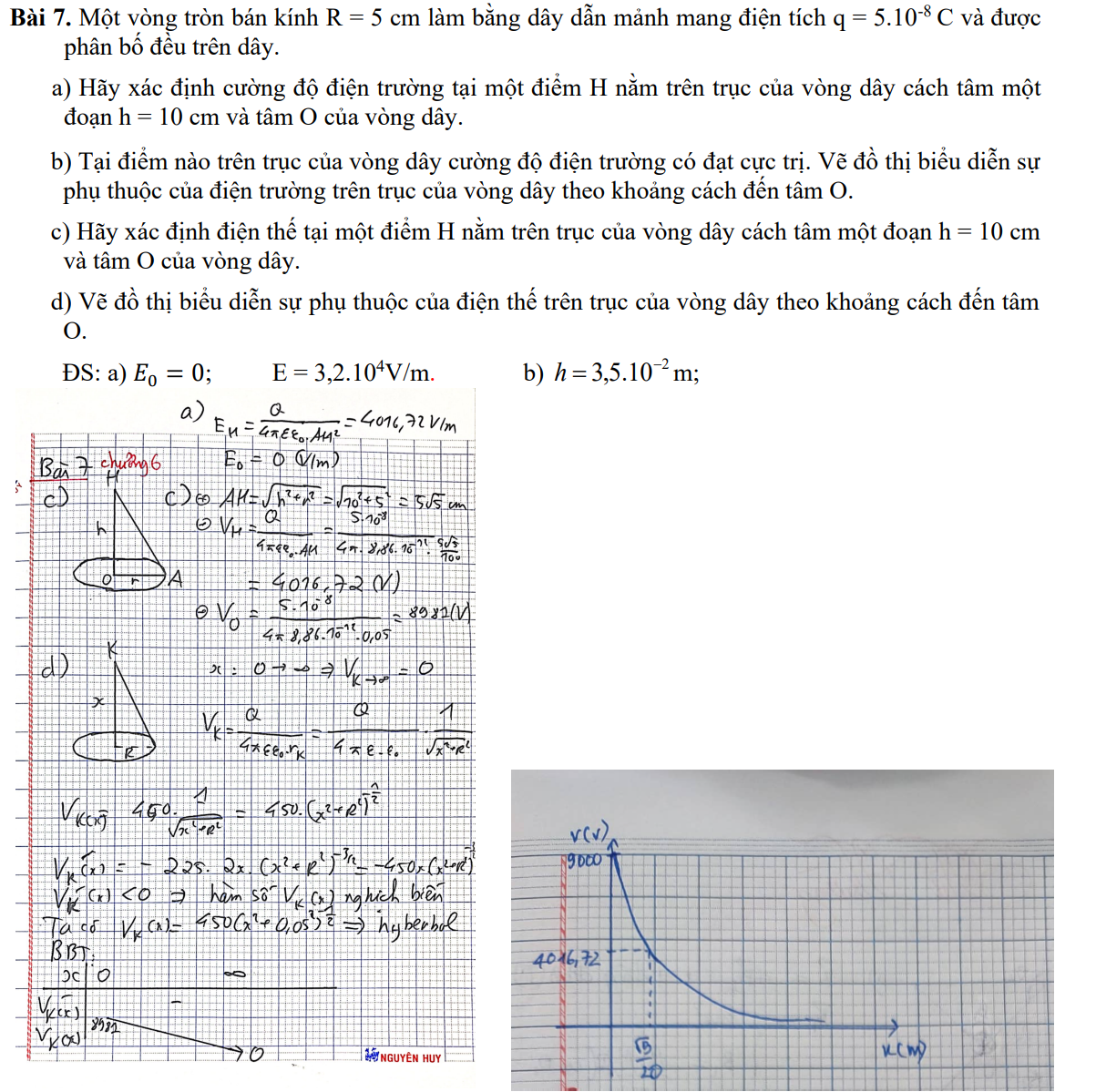
Chương 6: Điện trường (trường tĩnh điện):
- abc

Year 1: Semester 1

Conclusion Endterm

Thi trong 90p

Dùng Chung:

Công thức đổi tọa độ
Ma trận chuyển cơ sở

2 cách:
- dùng định nghĩa:
  - khác với tìm tọa độ của điểm ở trên, ở đây ta dùng các tọa độ nằm trong hệ cơ sở.
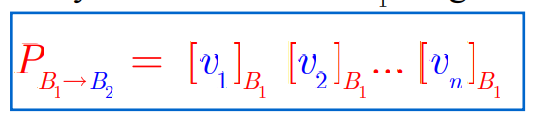
- dùng công thức chuyển cơ sở ma trận:
Web hack
- http://matrixcalc.org/en/

1. (2đ) chứng minh hệ vector là cơ sở của R^3, tọa độ đ/v cơ sở, vector con, cơ sở, số chiều

C/m 1 hệ vector là một cơ sở của R^3
- Chứng minh hệ là đltt và dim = dim không gian vector đó
- Cách chứng minh hệ vector đltt:
  - Det ≠ 0
  - or a*u1 + b*u2 + c*u2 = 0 và a = b = c = 0
C/m không gian vector là kgvt con của R^3
- Bước 1: C/m kgvt đó ≠ kgvt 0
- Bước 2: Đặt 2 ẩn, rồi áp vào điều kiện của kgvt
- Bước 3: Kết luận
Tìm cơ sở, số chiều của hệ vector/không gian vector
- hệ vector
- không gian vector
  - lấy một vector bất kì thuộc k/g,dựa vào điều kiện của hệ không gian, biến đổi…

2. (3đ) Ker, Im, cơ sở, số chiều

Chứng minh f là một axtt OR BIẾN ĐỔI TUYẾN TÍNH
- Bước 1: Gọi 2 biến x,y
- Bước 2: Biến đổi
- Bước 3: Kết luận
Tìm Ker và cơ sở, số chiều của Ker
- Bước 1: Cho các phần tử của hệ vector axtt = 0
- Bước 2: Tìm nghiệm theo ẩn
  - Có thể cần phải giải ma trận || hoặc đặt luôn x3 = t, rồi suy ngược nếu có thể
- Bước 3: Kết luận
Tìm Im và cơ sở, số chiều của Imf
- Bước 1: Thế các vector trong cơ sở chính tắc vào f, tìm Không Gian Sinh
- Bước 2: Giải ma trận dòng
- Bước 3: Kết luận ImF và dim(Imf)

3. (3đ) Chéo hóa ma trận, trị riêng, vector riêng

Trị riêng, vector riêng,tìm cơ sở để F đ/vs c/sở đó là m/trận chéo
Tìm ma trận astt
Draft cách tìm ma trận cũ

ví dụ ta cần tìm [f] |X,Y (X trên, Y dưới)

PHƯƠNG PHÁP TIÊU CHUẨN:

Ta lấy ví dụ để dễ nói chuyện: [f]x,y, x trên, y dưới
- ta lấy các giá trị trong cơ sở dưới (Y) vào hàm f() ra các vector mới
- gọi các vector mới là Vi, với i là số lượng các vector mới
- Giờ ta tính [Vi]x
  Từ đây, ta có 2 cách làm, tuy nhiên chủ yếu dùng công thức
  - Cách 1: dùng định nghĩa:
  - Cách 2: dùng công thức đổi tọa độ:
    - Giờ ta dùng công thức đổi tọa độ vector: [Vi]x
    - Nếu cơ sở cần đổi là chính tắc thì chỉ cần chuyển vị T
    - B2 trong hình ta lấy E
    - P (B->E) = ma trận nghịch đảo của P (E->B)
    - P (E->B) là các vector trong B chuyển thành dòng
- Nếu X,Y khác:
  - Nếu một trong 2 là cs chính tắc => dùng pptc hoặc cách cơ bản (dùng định nghĩa của đổi tọa độ):
    - Với (3;-2) là tọa độ theo cơ sở chính tắc
  - Nếu cả 2 đều ko là cschinh tắc: 2 cách
    - tìm ra vector mới rồi dùng định nghĩa
      
      vector mới = av1+bv2… = “vector mới khác”. a,b,c này ko phải là vector mới ở trên
    - Dùng công thức
      
      Tìm f(u1)B1, f(u2)B2 rồi ghép lại là ra

4. (2đ) Dạng toàn phương

Phương pháp lagrange biến đổi hệ toàn phương
- Trình bày: [pdf]

1. Tính tích phân suy rộng

Cách làm
- Bước 1: Nhìn xem có dùng được dạng đặc biệt:
  - Đặt t
  - Tích phân từng phần
- Bước 2

2. Xét sự hội tụ/phân kì của tpsr

3. Đạo hàm hàm nhiều biến, gồm : hàm (riêng/ẩn/hợp)

Cách làm
- Hiểu đề::
- Vài chỉ dẫn:
  - Nhìn cách làm sau:

4. giá trị lớn/nhỏ nhất hàm 2 biến trên miền bị chặn. Tìm Cực trị?

GTLN,NN
- XEM VÍ DỤ TẠI:
  - Link: [20211226]
  - vd1: lúc 1:04:00
  - vd2: lúc 1:09:50
- Bước 1: tìm nghiệm của đạo hàm theo x/y (đgl cực trị đ/v cấp 3)
  - TH1: tìm được nghiệm:
    - Thế các cặp số vào f, ta tìm được các giá trị F(x,y)
      
      Khá nhiều, ví dụ có 4 nghiệm x1,x2,y1,y2 => có 4 cặp nghiệm
  - TH2: Đạo hàm theo x,y ra pt 2 ẩn
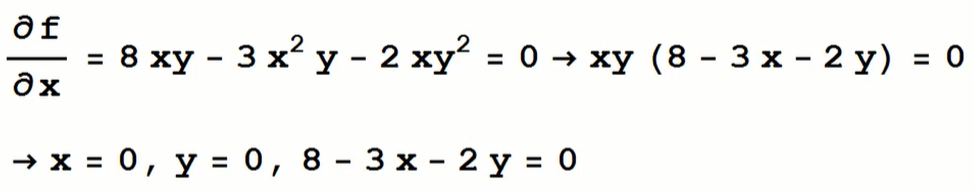
    - Sau đó kết hợp x trên với y/pt dưới, y trên với x/pt dưới
  - Chung Nhìn điều kiện, nếu x,y, (x,y) nào k thuộc thì loại
- Bước 2: tìm giá trị lớn nhất, nhỏ nhất trên biên
  - Tùy thuộc vào kiểu miền bị chặn,ta có các cách làm khác nhau:
    - x^2 + y^2 <= 4:
      
      => y^2 = 4 - x^2 và -căn(4) <= x <= căn(4)
      
      thay y^2 trên vào f(x,y), ta được hàm một biến
      
      Đọc tiếp ở Khi đã có hàm một biến
    - x = 0,y = 0,x + y = 6
      
      vẽ đồ thị x+y=6 ra, ta biết đc 0 <= x <= 6
      
      từ x+y = 6 => y = 6-x, thế y này vào f(x,y), được hàm một biến
      
      Đọc tiếp ở Khi đã có hàm một biến
    - x = 0; x = 1; y = 0; y = 2
      
      thế x = 0 vào f, đc pt theo y, rồi tìm min max hàm 1 ẩn như cấp 3, dùng đk 0 <= y <= 2
      
      tương tự, thế x = 1, y=0 , y=2
- Bước 3: So sánh các giá trị rồi tìm min, max
- Khi đã có hàm một biến:
  - Hàm một biến này cũng chính là f(x,y) mà gắn thêm pt đk vào vậy nên ta tìm min,max như cấp 3, rồi tìm giá trị min,max. Nếu nhận min,max này thì sẽ tìm y dựa vào đk rồi kết luận sau
  - Thế các x ở Bước 1 vào hàm 1 biến, ko cần quan tâm y vì hàm 1 biến lúc này chỉ có 1 ẩn x
Tìm cực trị
- Tìm nghiệm từ f’(x) và f’(y) rồi ghép lại thành các điểm
- Đặt A = f’‘(xx),B = f’‘(xy),C = f’'(yy)
- Thế các điểm vào: Δ = B^2 - AC
- Trong chương trình học của mình, nếu Δ >= 0 thì auto không phải cực trị
  - A < 0 -> cực đại, A > 0 -> cực tiểu:

5. Vẽ các mặt bậc 2 (mặt nón elliptic paraboloid,…),Phương trình tiếp diện, pháp tuyến tại điểm

Cách vẽ
1. Mặt elliptic paraboloid [ytb]: dạng z = x^2 + y^2
  - Cần xét 2 lần
    - Tại x=y=0, đc z, thì (x,y,z) này là đỉnh
    - Tại z =0,1,2… (1 cái là đủ) tìm các pt đường tròn khác, rồi nối mép đường tròn với đỉnh
2. Mặt nón [ytb]: z^2 = x^2 + y^2
  - => Từ đề suy ra z = ±căn(x^2 + y^2)
  - Cần xét 2 lần, rồi vẽ đối xứng là ra mặt nón còn lại:
  - z = 1 => x^2 + y^2 = … => vòng tròn
  - x = y = 0 => z = số, là đỉnh của mặt nón
  - Nối đỉnh với 2 mép vòng tròn là xong
3. Mặt elipsoid [ytb] x^2/a2 + y^2/b2 +z^2/c2 = 1
  - cần…
4. Trụ tròn [ytb] x^2/a2 + y^2/b2 = 1
5. Mặt cầu [ytb] x^2 + y^2 + z^2 = 9
Pt tiếp diện, pháp tuyến
- Chuyển hết pt qua một bên, rồi tìm đạo hàm:
- Nếu đề có 2 phương trình (tối đa là 2):
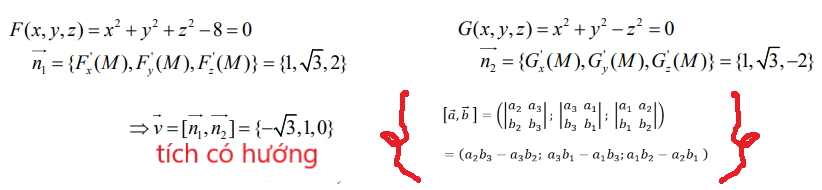
  - 3 giá trị ở trong vector mới là ứng với F’x,y,z trong công thức tính pt tiếp diện, pháp tuyến
- Pt tiếp diện (tiếp tuyến):
- Pt pháp tuyến (pháp diện):
- Dạng hơi lạ:
  - Cách giải:

Conclusion Midterm

Useful Links:

Name	Link
Matrix caculate	[matrixcalc.org] [Adjoint matrix calc]

Conclusion of Linear Alg

Khi nhân các ma trận

A * X = B <=> X = A^-1 * B
còn
X * A = B <=> X = B * A^-1

Các mẹo làm bài

hạng của A^-1 = hạng của A => ko cần tìm A^-1
Dùng ma trận con để tìm hạng ma trận lớn
det(A*B) = det(A) * det(B)
Có 2 cách c/m hệ là độc lập tt hay phụ thuộc tt

Procedure to solve determinant 4x4

Ways to find matrix rank

Transform the original into echelon one
Use determinant [pdf]

Ways to find reverse of matrixs

Use Laplace theorem [pdf]
Use elementary matrix transformation [pdf]

Exercises for chapter 3 : [pdf]
Useful Links:

Name	Link
Wolfram	[wolframalpha.com]
Symbolab, can show the steps for free	[symbolab.com]

Conclusion of Math analysis

Các mẹo làm bài

Tìm lim của đa thức có mũ chứa ẩn

Hàm số ngược

Inverse function [pdf]
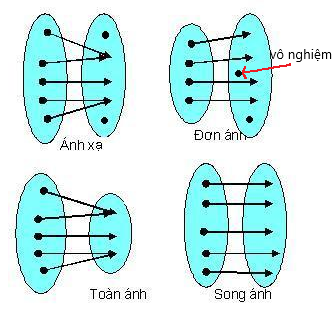
- song ánh là điều kiện cần và đủ để hàm số có hàm số ngược
Cách làm
- nếu đề cho luôn hàm số thì khỏe, còn nếu cho ánh xạ thì chú ý tập xác định của x,y
1. Kiểm tra nếu hàm là đơn ánh (có vị trí y ko tồn tại x) => không phải song ánh => ko có hàm ngược
  - vd: y = x^2, y < 0 => ko phải song ánh
2. Kiểm tra nếu hàm là toàn ánh (một y có nhiều x thỏa) => ko phải song ánh => ko có hàm ngược
  - y = x^2, với y > 0 có 2 nghiệm x => ko phải song ánh
3. Giải ra hàm ngược rồi ghi : vì pt luôn có nghiệm duy nhất với mỗi y, nên duy ra f-1(x) = …
  - y = x^2 với đk y >0, x>0 thì sẽ là song ánh
from the original one, transfer all the x into one side, e.g: y = x +1 => x = y-1
then transform all “x” symbol into “y”, and the same for “y” => y = x - 1.

Bài tập về liên tục, gián đoạn

1/x nếu x tiến đến 0- hoặc 0+ tức là 1/0.00001 -> vô cùng
- tốt nhất là bấm máy tính, cho x = 0.00000000001
Prove a function is continous at a point:
- CƠ BẢN: lim x->-x0 phải = lim x->+x0 và = 1 số thuộc R
- Vì hàm số đa thức luôn liên tục trên khoảng xác định, nên nếu đề kêu tìm all điểm gián đoạn thì chỉ xét tại vị trí đặc biệt
  - vị trí mẫu = 0 (điểm ko thuộc tập xác định), điểm giao của các khoảng.
- thường thì giới hạn trái, phải của một nhánh của hàm số phân nhánh sẽ = nhau, bị gián đoạn chủ yếu do nhánh khác tác động
- trường hợp hàm số chỉ có 1
- trường hợp hàm số gồm nhiều nhánh
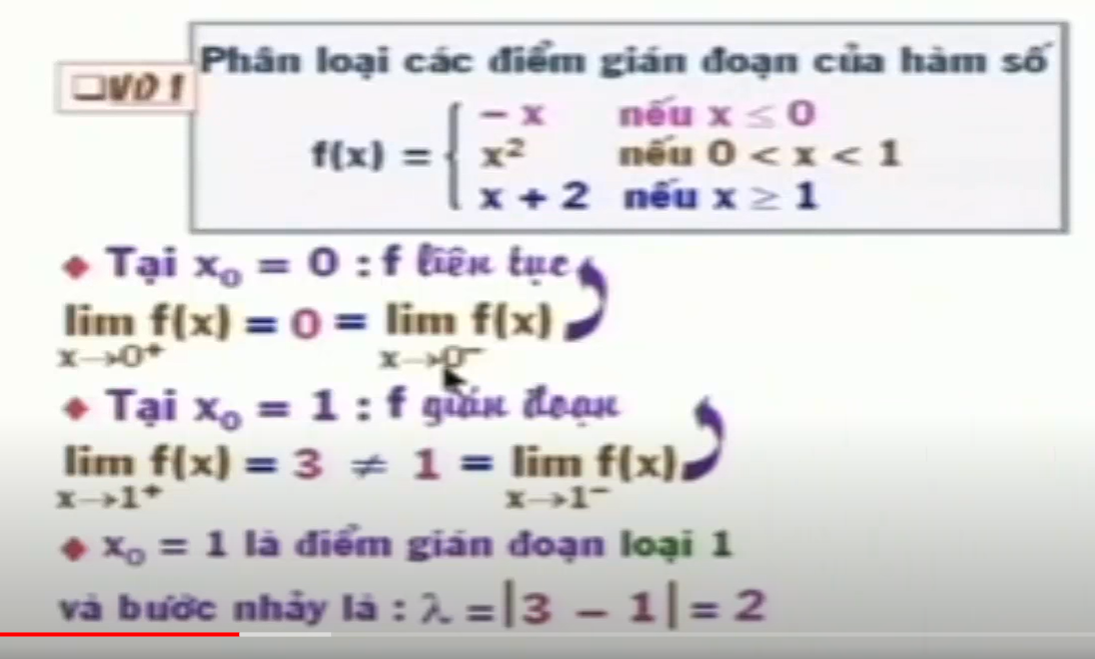
  - xem ví dụ là hiểu:
Các loại điểm gián đoạn
- điểm gián đoạn bỏ được
  - là khi lim x-> xo+ = lim x-> xo- = lim x->xo nhưng lim x->xo khác f(xo)
- điểm gián đoạn loại 1
  - khi lim x-> xo+ khác lim x-> xo-
- điểm gián đoạn lại 2
  - còn lại

PP giải Maclaurin

Khai triển tìm đạo hàm cấp 1,2,3,4…rồi thế x tìm đáp án
đạo hàm 2 vế đến khi ra cấp đạo hàm cuối,rồi thế x=0 vào các phương trình cũ, tìm dần các f’()

PP giải lebnitz

Nếu hàm là đơn thức thì đạo hàm 3-4 lần rồi tìm quy luật

Khả vi

Hàm liên tục chưa chắc khả vi, hàm khả vi auto liên tục
Để chứng minh khả vi tại 1 điểm ta chứng minh
- lim(x->xo) f(x) -f(xo)/x-xo = some value
- hoặc lim(x->-xo) f(x) - f(xo)/x-xo = lim(x->+xo) f(x) -f(xo)/x-xo
  - the same as f’(xo+) = f’(xo-)
- [Go to the website]
Đề bảo xét tính khả vi, ko nói cụ thể điểm thì xét các nghiệm của nó

Methods to solve lim exs

Nếu là hàm đa thức thì thử nhóm (x - xo) xem rút đc ko
VCB tương đương
- nếu tử/ mẫu là các tích thì ko cần tương đương toàn bộ
Lopitan

Note Books Sem1-Year1

Stop at page 60 file 2

Linear Algebra

Slide: [Slide 1]

Contents

Definitions:

Lesson 1
- Matrix
  - 3 Basics transformation of matrix [pdf]
- Echelon Matrix
- Invertible matrix [pdf]
  - Khả nghịch khi ma trận vuông có det khác 0 [pdf]
  - Cách tìm ma trận nghịch đảo: [pdf]
Lesson 2
- Submatrix and its rank
- Determinant (is a number created by using Phần bù đại số [pdf]
  - There is 7 properties (tính chất) [link]
  - Determinant of a echelon matrix [pdf]
  - Determinant of a block matrix [pdf]
  - Determinant of a product matrix [pdf]
  - Rules of Sarrus for 3x3 determinant [pdf]
- Laplace theorem [pdf]
  - Phần bù đại số
    - used to find reverse of matrix
  - Adjunct matrix (Ma trận phụ/liên hợp, use to find inverse of matrix)
    - Created by transpose a matrix created by many “Phần bù đại số” of the Main one. E.g: [pdf]
    - Adjunct matrix will be used to find reverse of matrix by Laplace treorem
- Matrix rank
Lesson 3
- Hệ pt Linear
  - Transform from hệ pt -> các ma trận hệ số (A), hệ số tự do (B) và ma trận ẩn số (X) => AX=B
- Hệ Cramer : a special kind of pt linear [9]
  - (n = m) & (det ≠ 0)
  - Chỉ có 1 ng duy nhất
  - Có khái niệm mới về Ma trận Aj [11]
- Cramer theorem [11]
  - a way to find all element of matrix X and it’s the only
- Biện luận số nghiệm ~~hệ Dạng Cramer~~ hệ có n = m (số ẩn = số hàng) [16]
  - Using DET
  - There is 3 possible circumstances [16]
  - We dont use detAj to biện luận, we try det A = 0 then find the value and check for the case
- Giải hệ (bất kì) bằng pp Gauss [25]
  - 3 steps [26]
  - Also first time encounter the term “Ma trận mở rộng” [26]
    - Ma trận mở rộng is also used in Kronecker theorem
  - Đoạn này có liên kết với Kronecker theorem
  - Lấy số ẩn - rank sẽ bằng số ẩn cần để tìm ra nghiệm
- Đk có nghiệm của hệ pt linear bất kì (Kronecker - Capelli theorem) [39]
  - Using rank of matrix
  - Nếu đổi cột thì ko được dính líu cột cuối
  - Đổi dòng bình thường
- Hệ pt Linear Thuần Nhất : Just like the normal one but B is all 0 [pdf]
  - Always có nghiệm là matrix of 0
  - đặc biệt là nếu số pt < số ẩn thì có vsn //check lại lí do
  - nghiệm cơ bản của pt thuần nhất
  - nghiệm tổng quát
  - Có 2 cách tìm nghiệm tổng quát
    - Tìm nghiệm tổng quát => nghiệm cơ bản
    - Tìm nghiệm cơ bản => nghiệm tổng quát
      - cần bn ẩn thì đặt bấy nhiêu bộ số để tìm số nghiệm cơ bản
Chương 3:Không gian vector
- Khái niệm không gian vector (KGVT): ko cần thuộc [pdf]
  - kgvt phải thỏa 8 t/c
  - 6 t/c khác của kgvt [pdf]
- Tập hợp các đa thức hệ số thực [pdf]
- Không gian véc tơ con [pdf]
- Dạng bài tập chứng minh một kg là kgvecto con của kgvt khác
  - cách 1: c/m một tập hợp là kgvt con của một kgvt khác [pdf]
  - ví dụ
  - cách 2
- Tổ hợp tuyến tính [pdf]
  - Dạng bài tập của cái này: Tìm biểu diễn tuyến tính, các ví dụ từ [pdf]
- Độc lập tuyến tính và phụ thuộc tt [pdf]
  - cách c/m hệ là đltt: hệ = 0 với mọi a = 0
  - cách c/m hệ là pttt: hệ = 0 mà có a khác 0
  - cách 1: dùng định nghĩa , cho a1*vector1 + a2… = 0 rồi tìm a
    - phù hợp với dạng hệ vector là hàm số
  - cách 2 (dùng det): [pdf]
    - det khác 0 thì là đltt, =0 thì là pttt
    - phù hợp dạng hệ vector là các vector dòng
  - Cách 3 (dùng rank), dùng ma trận của hệ vector [pdf]
    => Dạng bài tập chứng minh hệ độc lập/ phụ thuộc tuyến tính
- Định lí về hệ pttt [pdf]
  - Hệ vector có một vector 0 { {0,0};{1,2};{4,8} } thì auto là pttt
  - Hệ có 1 hệ nhỏ bên trong là pttt thì hệ lớn pttt
- Ma trận của Hệ vector [pdf]
  - cần tự đọc lại
- Bài 3: Số chiều, cơ sở của kgvt
  - Không gian sinh bởi một hệ vector
    - cách c/m một không gian ko phải hệ sinh của R^x [read the e.g]
  - Số chiều và cơ sở [pdf]
  - Dạng bài tập chứng minh hệ vector là hệ cơ sở kgvt của R^x
    - c/m hệ là đltt và dim = dim của R^x
    - định thức tạo bởi hệ có thể là ma trận dòng or cột vì định thức của ma trận dòng or cột đều như nhau
      - check lại slide 55, line 282 ở trên
  - Cơ sở chính tắc (quan trọng) [pdf]
  - Dạng bài tập Cách x/đ số chiều và cơ sở của kgvt [pdf]
    - số chiều = rank của ma trận dòng các vector trong hệ
    - nhận xét về cơ sở
    - E.G: [pdf]
- Bài 4: Tọa độ của vector [pdf]
  - Tọa độ của vector đối với một cơ sở , như hồi thpt,“tên tọa độ” = (x,y,z)
    - tự giải thích, hồi đó ta ghi tọa độ A = (x,y,z) tức là A= x*vectorI + y*vectorJ + z*vectorK, với i,j,k là các cơ sở chính tắc, giờ đây ta làm bài tập với các cơ sở khác
    - tọa độ được ghi dưới dạng ma trận cột, [the red one, with the ^T]
  - Dạng bài tập tìm tọa độ
    - e.g
      - vd1: [pdf]
      - vd3: [pdf]
        
        đừng đọc bài giảng, ghi khó hiểu quá, đơn giản là tìm giá trị của x ở cơ số B2, rồi lấy giá trị đó = với a*u1 + b*u2 rồi tìm a,b
    - đối với hệ vector là hàm thì ghi thẳng, ko có biến thành ma trận cột
  - Ma trận chuyển cơ sở [pdf]
    - tìm bằng cách dùng lí thuyết tọa độ của vector ở trên
    - 2 ma trận chuyển cơ sở lẫn nhau là ma trận nghịch đảo của nhau
    - quan trọng đặc biệt, chuyển từ không gian cơ sở chính tắc:[pdf]
  - Dạng bài tập tìm ma trận chuyển cơ sở
    - eg
      - vd4: [pdf]
  - Định lí đặc biệt công thức chuyển cơ sở ma trận: [pdf]
  - Công thức đổi tọa độ [pdf]
  - Dạng bài tập tìm tọa độ vector dựa vào công thức đổi tọa độ [pdf]
Chương 4: Ánh xạ tuyến tính : 5 điểm thi cúi kì
- Bài 1: Khái niệm ánh xạ tuyến tính [pdf]
  - phải thỏa mãn 2 điều kiện
    - Dạng bài tập c/m 1 cái (là/ko phải) axtt => phải thỏa mãn 2 cái trên
      - c/m là
        => thay vì xét 2 lần thì chỉ cần xét T(X+alphaY)
        
        khó ở chỗ ánh xạ này nhiều biến
      - c/m ko là:
        
        tìm 2 biến rồi c/m f(u+v) khác f(u) + f(v)
  - nhân/ảnh của axtt [pdf]
    - ker là tập hợp thuộc X để f(x) = 0, Ker(f) <= X
    - im là tập hợp f(x) với x thuộc X, Im(f) <= Y
    - Cách tìm Im(F) : < S > = X => < f(S) > = Im(f)
  - Định lí dimX = dimker + dimIm
  - Số khuyết/hạng của f [pdf]
  - Thuật toán tìm dim Ker và rank F [pdf]
- Bài 2: Ma trận của ánh xạ tuyến tính
  - Nếu không gian vector X = Y (R^n -> R^n) thì ánh xạ đó gọi là toán tử/phép biến đổi tuyến tính
  - Ma trận của axtt [pdf]
    - Công thức tìm nhanh m/trận axtt với cơ sở chính tắc [pdf]
  - Tính chất của astt: 2 cái [pdf]
  - Định lí chuyển đổi ma trận của astt
    - Chỉ quan tâm trường hợp đặc biệt [pdf]
- Bài 3: Trị riêng - vector riêng
  - Ma trận đồng dạng [pdf]
    - Tính chất của 2 ma trận trong toán tử tuyến tính [pdf]
  - Đa thức và pt đặc trưng
  - Dạng bài tập tìm pt đặc trưng của f
    - tìm A = [f]E
    - lấy đường chéo của ma trận trên - lamda
    - tìm lamda trong pt det = 0
  - Trị riêng, vector riêng
    - lamda là trị riêng của toán tử tuyến tính f khi
      - f(x) = lamda*x (x khác 0)
    - x ở pt trên gọi là vector riêng
    - Định lí về vector riêng,trị riêng [pdf]
      - Lamda là trị riêng của f khi và chỉ khi lamda là trị riêng của [f]B với b là một cơ sở
    - Chú ý phải nhớ: [pdf]
      - trong c/trình học, đa thức/pt đặc trưng của f auto = ma trận [f]B
      - các vector riêng của ma trận f ứng với các trị riêng khác nhau thì độc lập tt
  - Dạng bài tập Tìm trị riêng, vector riêng: 2 bước
    - [pdf]
    - Có ví dụ ở dưới
  - Không gian con riêng
    - là tập hợp các vector x (kể cả vector 0) thỏa f(x) = lamda*x
    - pic46
    - E(lamda) là không gian con riêng ứng với lamda
  - Dạng bài tập tìm không gian con riêng
    - là hệ sinh tạo bởi các vector cơ sở tính ra được ứng với mỗi lamda
  - Định lý Cayley – Hamilton không cần học vì hiếm ra
- Bài 4: Chéo hóa ma trận vuông
  - Khái niệm
    - cho toán tử tuyến tính f, gọi A là ma trận [f]B với B là một cơ sở nào đó
    - A gọi là chéo hóa được nếu A đồng dạng với ma trận đường chéo DET
      - tức là P^-1 * A * P = D
    - P,D là gì và cách tìm, đọc ở [pdf]
    - khi đó ta nói P làm chéo hóa ma trận A
  - Điều kiện chéo hóa được [pdf]
    - CHÚ Ý HỆ QUẢ, sẽ dùng trong thi
  - Ma trận làm chéo hóa ma trận vuông LÀ GÌ [pdf]
    - Trong đây giải thích ý nghĩa trong công thức ở khai niệm chéo hóa ma trận
      - P^-1 * A * P = D
  - Dạng bài tập Thuật toán chéo hóa ma trận vuông [pdf]
    - đi tìm trị riêng, nếu ko có thì => ko chéo hóa đc
- Bài 5: Dạng toàn phương:
  - Ánh xạ song tuyến tính [pdf]
  - Ma trận dạng song tuyến tính: f(x,y) = X^T * A * Y [pdf]
    - Ma trận A: là các thành phần của f(x,y) tạo thành ma trận [pdf]
  - Dạng toàn phương: là dạng đb của axsong tt page13
  - Biến đổi dạng toàn phương về chính tắc
    - Phương pháp Lagrange [pdf]
      - Có 2 dạng
  - Dạng chuẩn tắc của dạng toàn phương
  - Dấu của dạng toàn phương [pdf]

Mathematical analysis

Contents

Definitions:

Chapter 1: Số thực
- Ánh xạ [pdf]

Chapter 2: Hàm số biến số thực
- Inverse function [pdf]
  - song ánh là điều kiện cần và đủ để hàm số có hàm số ngược
- Redefine the meaning of lim, [pdf] //check this later

Chapter 3: Giới hạn và sự liên tục của…
- Some examples to remove the dạng vô định [pdf]
- Apply some results to solve problem [pdf]
  - Đẳng thức (3.1) [end of 78]
  - Đẳng thức (3.2) tại [pdf]
  - Đẳng thức (3.5) tại [pdf]
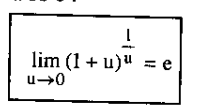
    - it’s 1^infi
    - lim của mũ (bỏ cái 1/u) bằng bn thì là mũ của e
  - Đẳng thức khác:
- Giới hạn một phía
- Vô cùng lớn/bé
  - In the Too large case,it’s contain both -∞ and +∞
  - There is a feature between VCL and VCB [pdf]
  - Tốc độ hội tụ về 0, Tốc độ tiến ra vô cùng
    - Sự tương đối (bậc) của hai VCB (Hoặc VCL)
      - Nếu 2 hàm là tương đối với nhau thì có thể đổi chỗ trong một lim [end of page 88]
      - Biến đổi giữa các VCB tương đương [end of page 88]
        
        [Youtube]
- Another way to write LIM using VCB,VCL [page 89]
- Hàm số liên tục
- Chứng minh một số công thức [page 93], xem lại đoạn 02:10:00
- Điểm gián đoạn [pdf]
  - có 3 loại:
    - loại 1: [pdf]
      - Bước nhảy là trị tuyệt đối |fx->xo+ - fx->xo-|
    - loại 2: f(xo) ko thuộc R
      - nếu x->xo tạo ra 1/0 = ∞
      - nếu x->xo+1 hoặc x->xo-1 là dạng đặc biệt như ∞
    - loại 3: gián đoạn bỏ được, gặp trong hàm số nhiều trường hợp
- Các tính chất của hàm số liên tục
  - định lí 3.7 [pdf]

Chương 4 đạo hàm vi phân
- Đạo hàm là gì [pdf]
  - định nghĩa đạo hàm
- đạo hàm của hàm số ngược - định lí (4.3) [pdf]
  - từ đây tìm đc đạo hàm của arcsin,…
- Vi phân [pdf]
  - đạo hàm theo tham số
- Đạo hàm một phía, đạo hàm vô cùng
  - muốn tồn tại đạo hàm thì đạo hàm trái = đạo hàm phải [pdf]
- Đạo hàm, vi phân cấp cao
  - tìm f đạo hàm n lần bằng cách đạo hàm cấp 2, 3 rồi tìm quy luật
- quy tắc lebnitz [pdf]

Chương 5 Các định lí về giá trị trung bình
- Định lí fermit [pdf]
- Định lí Lagrange [pdf]
  not important
- Định lí Cauchy [end of 146]
- Định lí mở rộng của Lagrange , created Taylor formula[pdf]
  - Công thức taylor
    - Khi c = 0 thì đgl công thức mac laurin
- Mac Laurin giúp đổi hàm số bất kì thành các đa thức [pdf]
  - We can use the resolve of mac laurin as vcb tương đương
- Quy tắc lopitan [pdf]
  - chỉ dùng đc khi lim f(x)/g(x) = 0/0 || ∞/∞
- Khảo sát sự biến thiên hàm số [pdf]
  - ko dạy lại vì đã dạy ở c3
- Đường cong cho dưới dạng tham số [pdf]
  - chưa đi sâu
  - đường tròn cycloid [pdf]
- Hệ tọa độ cực [pdf]
  - Hệ tọa độ đề các => Hệ tọa độ cực ( x, y biến đổi theo r, phi )
Chương 6 Nguyên hàm, tích phân:
- Các pp giải tích phân
  - đổi biến [pdf]
    - phải đạt giới hạn của biến t để nó là song ánh (với 1 giá trị t chỉ cho duy nhất 1 nghiệm x)
  - tích phân từng phần [pdf]
- Tích phân của phân thức hữu tỉ P(x)/Q(x) [pdf]
  - Có 2 dạng phân thức: Thật sự và Không thật sự
  - Nếu phân thức gốc là không thật sự,nó luôn có thể biến đổi thành đa thức + phân thức thật sự
    =>đa thức thì quá dễ, ta chỉ cần đi tìm nguyên hàm của phân thức thật sự
    - NOTE NHẸ: cách chia đa thức cho đa thức: a/b = q + r/b : r là số dư (a = b*q + r)
  - 2 trường hợp phân thức thật sự thường gặp:
- Định lí 6.3: có thể phân tích đa thức thành các tích đa thức [pdf]
  - hai phân thức trên cũng thuộc định lí (và kết quả của đ/li) này
  - chỉ cần đi tìm các tử số
  - Cách của thầy và trong sách như nhau, đều là quy đồng vế phải, rồi lấy tử trái = tử phải để tìm các ẩn
    - Điểm khác là trong sách là đồng nhất hệ số, còn thầy là thế x vào để triệt tiêu dần.
  - Sau khi có các tử thì thế vào công thức để ra nguyên hàm (là đáp án cần tìm của bài toán tích phân)
  - Khi tách phân thức thành nhiều phân thức, nếu mẫu là một đa thức không có nghiệm nguyên thì thử phải là đa thức bậc 1
- Phương pháp giải tích phân lượng giác:
  - đặt t = tan x/2
    => sinx = 2t/(1+t^2)
    => cosx = (1-t^2)/(1+t2)
    => dx = 2dt/(1+t^2)
Chương 7: Tích phân xác định:
- Kiểm tra cuối kì là chương 7,8,9
- Hình thang cong là gì [pdf]
  - Cách tính diện tích
- tính độ dài đường cong phẳng AB [chưa xác thực]
- công thức thể tích vật tròn xoay [7.83]
- tích phân suy rộng (quan trọng) - đề có 5 câu, 2 câu thuộc phần này
  - có 2 loại
    - loại có tích phân chạy đến vô cùng
    - loại có tp hữu hạn và hàm số k bị chặn
  - TH1 Cận trên tích phân là vô hạn: [pdf]
    - tích phân suy rộng: hội tụ, phân kì
      - tích phân đgl hội tụ khi tích phân có giá trị hữu hạn
      - phân khi khi giá trị là vô cùng
      - có thể tưởng tượng về mặt hình học, hội tụ khi diện tích thu nhỏ lại, và ngược lại
  - TH2 Cận trên là hữu hạn
    - có 3 trường hợp điểm bất thường (là điểm thế vào ko có nghĩa) nằm trên hoặc dưới VÀ BẤT THƯỜNG CẢ TRÊN/DƯỚI
    - Cũng gọi là t/p suy rộng và cũng có hội tụ, phân kì
      - hội tụ khi tính được tích phân hữu hạn, x/định
      - phân kì khi tích phân k tồn tại hoặc bằng vô cùng ∞
    - e.g
- Dạng bài tập tìm ẩn để tích phân là t/p hội tụ/phân kì
  - giải ra theo ẩn rồi xét trường hợp
- (ĐL 7.9) dùng cho tích phân suy rộng loại 1 [pdf]
  - Tính chất 1: “Bé hơn Hội Tụ thì Hội Tụ, Lớn hơn Phân Kì thì Phân Kì”
    - chỉ đúng theo quy luật này.
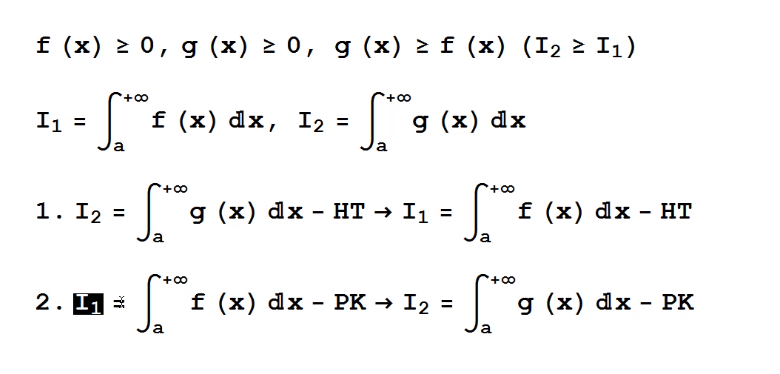
  - Tính chất 2: tử và mẫu cùng loại
    - lim chia nhau = 0<k<vô cùng => cùng loại
    - mẹo dùng:
      - tìm g(x) mà tính được, thường lấy 1/x^alpha
- Ghi nhớ tích phân a->vô cùng 1/x^a dx vì thường xuyên dùng để dùng định lí 7.9/2
- Ghi nhớ 2 tích phân suy rộng loại 2 sau:
- (ĐL 7.10) dùng cho tích phân suy rộng loại 2
  - Tính chất 1: giống 7.9
  - Tính chất 2: khác tính chất 7.9 [pdf]
    - lim chia nhau = 0 và g(x) hội tụ thì sẽ cùng hội tụ, ko dùng cho p/kìm
    - lim chia nhau = vô cùng và g(x) phân kì thì…
    - mẹo dùng:
      - tìm g(x) mà tính được, thường lấy 2 tích phân suy rộng loại 2 ở trên
- Tóm lại, nếu đề hỏi tích phân là hội tụ hay phân kì thì có 4 cách làm:
  - cách 1: giải tích phân rồi dùng định nghĩa của hội tụ/phân kìm
  - cách 2: dùng định lí 7.9 - 7.10
  - cách 3: tích phân từng phần,đổi biến
  - cách 4: tách tích phân thành 2 cái, rồi dùng định lí hội tụ + hội tụ = hội tụ… [pdf]
- Bài tập 21,22 trang 333

Sách khác

Chương 8: hàm số nhiều biến
- Tập hợp Liên Thông: 2 trường hợp [Some first lines]](…/…/…/…/savefiles/giaitich_tap3.pdf#page=5)
  - Đơn liên
  - Đa liên nếu có tập khác nằm ở trong
- Miền xác định của hàm [pdf]
- Đạo hàm riêng [pdf]
  - Hàm số f(x,y) có 2 đạo hàm, đạo hàm theo biến nào thì biến kia là tham số
  - Có công thức đạo hàm bằng cách đặt u,v
- Vi phân của hàm số 2 biến
  - Số gia
  - Công thức vi phân: [df = f’x *dx + f’y *dy]
- Đạo hàm cấp cao [pdf]
  - Đạo hàm hỗn hợp
  - Đạo hàm cấp cao: Có thể thay đổi biến đạo hàm
    - ví dụ:
      - lần 1 đạo hàm là theo x -> ghi x nhỏ ở dưới
      - lần 2 đạo hàm theo x -> x*x = x^2
      - lần 3 đạo hàm theo y -> x^2*y
- Định lí 1.3 áp dụng cho all bài [pdf]
  - f’‘(x,y) = f’'(y,x)
- Vi phân cấp cao:
  - chính là vi phân của vi phân cũ [pdf]
  - Công thức:
    d^2(f) = d(df) = (df)'theo x*dx + (df)'theo y*dy
- Hàm số thuần nhất
  - Yêu cầu thỏa mãn 1.7: [pdf]
  - Định lí euler 1.8 [pdf]
    - giúp nhận biết hàm là thuần nhất hay ko
  - Tính chất:
    - Nếu F là hs thuần nhất bậc k thì đạo hàm riêng cấp 1 là thuần bậc k-1
- Công thức taylor [pdf]
- Cực trị [end page]
  - Nếu (x,y) là một cực trị thì đạo hàm f’(x) và f’(y) đều = 0 tại (x,y)
- Dạng bài tập tìm cực đại, tiểu
  - Dùng phương pháp của thầy (cũng chính là trong sách, nhưng thầy thì đi chứng minh (taylor đến bậc 2)
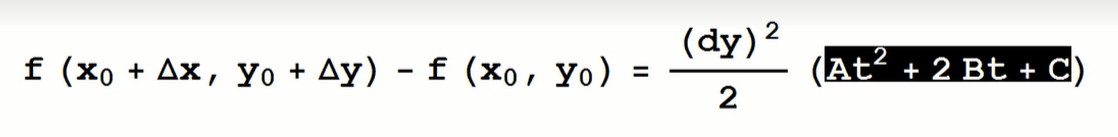
    - Đạo hàm theo x,y tìm nghiệm
    - A = f’‘(xx),B = f’‘(xy),C = f’'(yy)
    - Ta tìm Δ = B^2 - AC của tam thức bậc 2 trên
      - Trong chương trình học, nếu Δ>= 0 thì auto không phải cực trị
      - A < 0 -> cực đại, A > 0 -> cực tiểu
- Gía trị lớn nhất, nhỏ nhất trên miền bị chặn
  - Dạng bài tập tìm gtln,nn
    - đầu tiên tìm ra các cặp nghiệm của đạo hàm theo x/y
      - thế các cặp số vào f để tìm giá trị
    - sau đó tìm giá trị lớn nhất, nhỏ nhất trên biên
      - biến đổi x/y theo biến kia bằng điều kiện của miền bị chặn
      - thế vào hàm số
      - tìm min,max của nó (giống hồi cấp 3)
    - Từ đây so sánh các giá trị
- bài tập 28 trang 51
- Khái niệm hàm số ẩn, cực trị có đ/kiện [end page]
  - hàm số ẩn ở đây là một h/s suy ra được từ hàm số chính
- Định lí 1.9
  - F có đạo hàm theo y -> tồn tại pt y theo x
- Đạo hàm của hàm số ẩn
  - F(x,y)
    - y’ = - F’(x) / F’(y)
  - F(x,y,z)
    - z’(x) = - F’(x)/F’(z)
    - z’(y) = - F’(y)/F’(z)
      -> Chú ý nhìn sẽ ra quy luật
      -> a’(b) = - F’(b)/F’(a)
- Cực trị có điều kiện
- Đường [endpage]
  - xo = x(t), A = x’(t)
  - PT tiếp tuyến: x-x0 /A = y-y0 /B = z-z0 /C
  - PT pháp diện: A(x-x0) + B(y-y0) +C(z-z0) = 0
- Mặt: có trong thi cuối kì [pdf]

Marxist philosophy

Contents

Definitions:

Buổi 1
- Nguồn gốc của triết học nói chung [pdf]
  - Nguồn gốc nhận thức
  - Nguồn gốc xã hội
    - Ban đầu ra đời để bảo vệ giai cấp thống trị, sau này phát triển lên, nhiều người phát triển nó để bảo vệ quyền lợi cho cả giai cấp thấp
- Khái niệm triết học
- Đối tượng (nghiên cứu) của triết học [pdf]
  - Tùy vào các thời đại
- Thế giới quan
  - Vai trò
- Những vấn đề cơ bản của Triết Học
  - Tìm hiểu mqh giữa vật chất <-> ý thức
    - => Chủ nghĩa duy vật
      - Có 3 cấp độ (phát triển theo thời gian) [pdf]
      - Khả Tri Luận
    - => Chủ nghĩa duy tâm
      - Có 2 loại [pdf]
      - Bất Tri Luận
- Khái niệm Biện Chứng / Siêu Hình [pdf]
Buổi 2
- Vai trò của triết học
- Nguồn gốc ra đời triết học Mác le-nin [pdf]
  - Đk kt xã hội
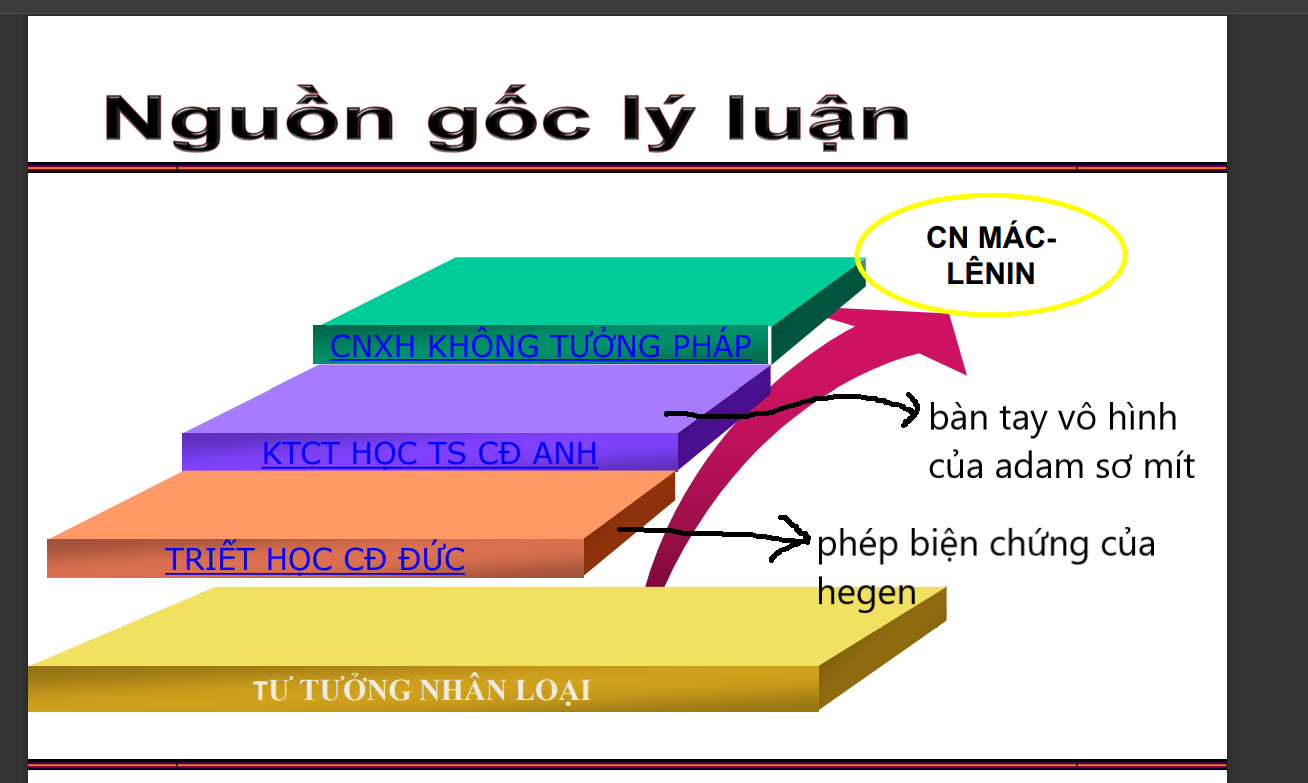
  - Nguồn gốc lý luận ( triết học mác dựa vào cái gì để nói lên quan điểm?)
  - Nhân tố chủ quan [pdf]
  - Ba thời kỳ quan trọng trong phát triển
- Các cống hiến của triết học Mác (cho triết học in general, cho xã hội)
- Leenin đóng vai trò gì
  - phát triển học thuyết mác
  - ứng dụng nó để phát triển xã hội chủ nghĩa mới do ông cách mạng thành công
- Khái niệm Triết học Mác Lenin [pdf]
  - Đối tượng nghiên cứu của triết học Mác-lenin
- Chức năng của Triết học Mác-lenin
Buổi 3
- Quan niệm chủ nghĩa duy vật thời cổ đại
  - Phương Đông: Ấn độ, Trung Quốc
  - Phương Tây: Hy lạp
  - Tích cực/ Hạn chế
- Sự phá sản của các quan điểm duy vật siêu hình về vật chất
- Định nghĩa vc của lênin
- Ý nghĩa đn vc của lênin
- Các hình thúc vận động
- Nguồn gốc ý thức
  - Bản chất của ý thức
  - Kết cấu của ý thức
Buổi 7
- Quy luật cơ bản của phép biện chứng duy vật

Prepare for lesson

Buổi 3
- Ques 1:
  - Ấn độ
    - SàmKhya https://youtu.be/IJqJQAjrK2M?t=117
    - Nyaya - Vaisesika https://youtu.be/IJqJQAjrK2M?t=135
      - đất, nước, lửa, gió => tạo từ nguyên tử, khá giống democrot
    - Phật giáo https://youtu.be/IJqJQAjrK2M?t=235
  - Trung quốc
    - Thuyết âm dương https://youtu.be/IJqJQAjrK2M?t=274
    - Thuyết Ngũ Hành https://youtu.be/IJqJQAjrK2M?t=371
      <--------------
  - Hy lạp
    - Thales - nước https://youtu.be/IJqJQAjrK2M?t=661
    - Anaximander - apeiron https://youtu.be/IJqJQAjrK2M?t=704
      - học trò thales
    - Anaximenes - không khí
      - học trò anaximander
    - Heraclitus - lửa
    - Democritus - nguyên tử https://youtu.be/IJqJQAjrK2M?t=893
- Ques 2:
  [Link]
- Ques 3: https://www.youtube.com/watch?v=6MiWq8ab7Xo
  - ko định nghĩa theo pp thông thường
  - đặt vc >< ý thức
  - vật chất ở đây khác vật chất trong các môn khoa học khác
  - như ở trên , vật chất độc lập với ý thức, vật chất tác động ý thức tạo ra cảm giác
    và với ý trên, leenin khẳng định vật chất có trước ý thức
  - “…chép lại, chụp lại, phản ảnh” => con người có khả năng nhận thức thế giói
  - khắc phục được khủng hoảng khoa học lúc đó
  - tách biệt khái niệm vật chất triết học với vc khoa học
  - giải quyết được câu hỏi vật chất trong triết học dựa trên duy vật biện chứng
  - mở rộng sang cả lĩnh vực xã hội
- Ques 4:
- Ques 5:
  - https://www.facebook.com/groups/376625993226816/posts/603475680541845
- Ques 6:
  - nguồn gốc tự nhiên
    - bộ não người
    - sự tác động của thế giới khác quan lên não người
  - nguồn gốc xã hội
    - lao động
    - ngôn ngữ
      Câu 6: Nguồn gốc của ý thức? nguồn gốc nào là quyết định nhất? Vì sao?
Buổi 4
- Câu 1: Làm rõ nội dung nguyên lý mối liên hệ phổ biến (khái niệm, tính chất, ý nghĩa)? cho ví dụ minh họa về liên hệ phổ biến.
  - Khái niệm:
    - Ở mỗi quan điểm (siêu hình, duy tâm, dtbc) là khác nhau
      - Siêu hình: Các sự vật, sự việc, hiện tượng tồn tại tách rời cô lập nhau, cái này bên cạnh cái kia, giữa chúng không có sự phụ thuộc liên hệ lẫn nhau.
      - Duy tâm: cơ sở của sự liên hệ tác động qua lại giữa các sự vật hiện tượng là ở lực lượng siêu tự nhiên
    - Mối liên hệ giống như liên hệ (sự tác động qua lại của 2 đối tượng), khác là ở đây nhiều hơn 2 đối tượng
      - từ phổ biến có nghĩa là xảy ra rộng rãi
      - Mối liên hệ phổ biến (MLHPB) là mối liên hệ nhưng đối tượng ở đây có thể là cả ý thức và vật chất
  - Tính chất:
    - Tính khách quan: MLHPB tồn tại độc lập với con người, chúng ta chỉ nhận thức được nó
    - Tính đa dạng, phong phú, muôn vẻ : mọi sự vật, hiện tượng đều có những mối liên hệ cụ thể và chúng có thể chuyển hóa cho nhau; ở những điều kiện khác nhau thì mối liên hệ có tính chất và vai trò khác nhau
  - Ý nghĩa: 3 ý
    - Khi giải quyết 1 vấn đề cần xem xét các yếu tố cấu thành liên hệ mật thiết, phải xem xét yếu tố lịch sử hình thành trong mối tương quan với hiện tại
      - còn gọi là Quan điểm toàn diện
    - Chống quan niệm siêu hình
      - Không thấy được trọng tâm, trọng điểm, đánh giá tràn lan các mối liên hệ , không thấy đâu là chủ yếu đó là siêu hình. Chống chủ nghĩa chết chung và thuận nghị biện. Trong đó, chủ nghĩa chết chung là Kết hợp 1 cách vô nguyên tắc giữa các sự vật hiện tượng.
    - Để cải tạo sự vật thì phải có giải pháp đồng bộ, toàn diện. Chọn lĩnh vực nào là chủ yếu
      - ví dụ Trong Công tác quản lý thì phải phân cấp quản lý.
      - Ví dụ: nhà nước (bộ ban ngành), cơ quan (phòng, ban)
  - Ví dụ:
    - Cá ko thể sống thiếu nước
    - Cung và Cầu trong bán hàng tác động lẫn nhau
- Câu 2: Làm rõ nội dung nguyên lý Phát triển (khái niệm, tính chất, ý nghĩa)? Cho ví dụ minh họa về Phát triển.
  - Khái niệm:
    - Siêu hình:
      - là sự thay đổi về lượng, ko về chất
    - Biện chứng:
      - Phát triển là (một phạm trù triết học) quá trình vận động của sự vật theo khuynh hướng đi lên từ thấp đến cao, từ đơn giản đến phức tạp, từ kém hoàn thiện đến hoàn thiện hơn.
  - Tính chất:
    - Tính khách quan: nguồn gốc của sự phát triển do các QL khách quan chi phối mà cơ bản nhất là QLMT
    - Tính phổ biến: Sự phát triển diễn ra ở trong mọi lĩnh vực, mọi sự vật, hiện tượng, mọi quá trình và giai đoạn của chúng và kết quả là cái mới xuất hiện
    - Tính phong phú, đa dạng: Quá trình phát triển của sự vật, hiện tượng không hoàn toàn giống nhau, ở những không gian và thời gian khác nhau; chịu sự tác động của nhiều yếu tố và điều kiện lịch sử cụ thể
  - Ý nghĩa:
    - Dựa vào nguyên lý về sự phát triển, ta có cơ sở lý luận khoa học để định hướng việc nhận thức thế giới và cải tạo thế giới
    - Để nhận thức và giải quyết được bất cứ những vấn đề gì trong thực tiễn thì một mặt cần phải đặt sự vật theo khuynh hướng đi lên của nó.
      - e.g: ko thể đào tạo động vật để nói chuyện được với người
        có thể đào tạo em bé sơ sinh thành kỹ sư
    - Xem xét sự vật phải biết phân chia quá trình phát triển thành các giai đoạn
    - Trong hoạt động nhận thức và trong hoạt động thực tiễn của con người cần phải tôn trong quan điểm phát triển
      => phát hiện và ủng hộ cái mới, chống bảo thủ
  - Ví dụ:
    - tổ chức xã hội loài người từ Thị tộc, bộ lạc đến những tổ chức xã hội cao như bộ tộc, dân tộc
    - hạt giống sau khi phát triển to lên thì được gọi là cái cây
    - học sinh khi lên đại học được gọi là sinh viên
Buổi 5
- Câu 1: Làm rõ nội dung phạm trù cái chung, cái riêng?
  - Khái niệm:
    - Cái chung, cái riêng là phạm trù trong phép biện chứng duy vật Mác-Lenin
      - Cái chung chỉ những mặt, những thuộc tính, yếu tố, quan hệ tồn tại phổ biến trong nhiều sự vật, hiện tượng
      - Cái riêng để chỉ một sự vật, hiện tượng, một quá trình nhất định.
  - Tính chất:
    - Cái riêng, cái chung tồn tại khách quan nhưng giữa chúng vẫn mối liên hệ với nhau
    - Cái chung chỉ tồn tại trong cái riêng, thông qua cái riêng mà biểu hiện sự tồn tại
    - Ko có cái riêng nào tồn tại tuyệt đối độc lập
    - Cái riêng phong phú hơn cái chung, nhưng cái chung sâu sắc hơn cái riêng
  - ý nghĩa:
    - Muốn nhận thức được cái chung, cái bản chất thì phải xuất phát từ cái riêng
    - Nhiệm vụ của nhận thức là phải tìm ra cái chung và trong hoạt động thực tiễn phải dựa vào cái chung để cải tạo cái riêng
  - ví dụ:
    - không có doanh nghiệp nào có thể tồn tại mà lại không tuân theo các quy tắc chung của thị trường
    - nông dân Việt Nam có cái chung với nông dân các nước khác là đều là các tư hữu nhỏ, sản xuất nông nghiệp, sống ở nông thôn v.v., còn cái riêng là chịu ảnh hưởng của văn hoá làng xã, áp dụng ít máy móc, chủ yếu dùng sức người,gia súc
- Câu 2: Làm rõ nội dung cặp phạm trù nguyên nhân, kết quả? Cho ví dụ minh họa.
  - Khái niệm:
    - Cả 2 là một cặp phạm trù trong phép biện chứng duy vật của chủ nghĩa Mác-Lenin
      - Nguyên nhân là sự tác động lẫn nhau giữa các mặt trong một sự vật, hiện tượng hay giữa các sự vật, hiện tượng với nhau gây ra một hoặc hơn một sự biến đổi nhất định.
      - Kết quả là sự biến đổi xuất hiện do sự tác động lẫn nhau của các mặt trong một sự vật, hiện tượng hoặc giữa các sự vật, hiện tượng với nhau
  - Tính chất: 3
    - Tính khách quan,Tính phổ biến, Tính tất yếu
      - tính tất yếu: nguyên nhân ở mỗi đk cụ thể sinh ra kết quả khác nhau
  - Mối quan hệ biện chứng:
    - Nguyên nhân sản sinh ra kết quả.
    - Kết quả có thể tác động lại nguyên nhân:
    - Ví dụ: Nhúng một thanh sắt vừa mới nung đỏ vào chậu nước nguội, thì nhiệt độ của nước trong chậu sẽ tang lên. Sau đó, nước trong chậu do tăng nhiệt độ sẽ kìm hãm tốc độ tỏa nhiệt của thanh sắt.
  - Ý nghĩa:
    - Trong hoạt động nhận thức và hoạt động thực tiễn phải bắt đầu từ việc đi tìm những nguyên nhân xuất hiện sự vật, hiện tượng
    - Cần phải phân loại các nguyên nhân để có những biện pháp giải quyết đúng đắn.
    - Phải tận dụng các kết quả đã đạt được để tạo điều kiện thúc đẩy nguyên nhân phát huy tác dụng, nhằm đạt mục đích đã đề ra.
  - Ví dụ:
    - chiếc dùi đập lên ᴠà mặt trống là nguуên nhân của tiếng trống kêu. Tiếng trống kêu là kết quả của ѕự tác động giữa chiếc dùi ᴠà mặt trống
    - giai cấp vô sản mâu thuẫn giai cấp tư sản => cách mạng vô sản
- Câu 3: Làm rõ nội dung cặp phạm trù Nội dung và hình thức? cho ví dụ minh họa.
  - Khái niệm:
    - Nội dung và hình thức là một cặp phạm trù trong phép biện chứng duy vật của chủ nghĩa Mác-Lenin
      - Nội dung là tổng hợp tất cả những mặt, những yếu tố, những quá trình tạo nên sự vật
      - Hình thức là phương thức tồn tại và phát triển của sự vật, là hệ thống các mối liên hệ tương đối bền vững giữa các yếu tố của nó
  - Mối quan hệ biện chứng giữa chúng:
    - Nội dung và hình thức thống nhất và gắn bó khăng khít với nhau.
    - Nội dung quyết định hình thức.
      - Ví dụ:
        
        Nội dung quan hệ giữa anh A và chị B là quan hệ bạn bè, khi đó hình thức quan hệ giữa hai người không có “giấy chứng nhận”. Khi anh A và chị B kết hôn, nội dung quan hệ bị thay đổi, lúc này hình thức quan hệ cũng thay đổi theo và hai người có “giấy chứng nhận kết hôn”.
    - Hình thức không thụ động mà tác động trở lại nội dung
  - Ý nghĩa:
    - Không tách rời nội dung với hình thức
    - Cần căn cứ trước hết vào nội dung để xét đoán sự vật.
    - Phải theo dõi sát mối quan hệ giữa nội dung và hình thức.
    - Cần sáng tạo lựa chọn các hình thức của sự vật.
  - Ví dụ:
    - Nội dung của chiếc xe hơi là có 04 bánh cao su, chở được nhiều người
      - Hình thức của chiếc xe hơi là các bộ phận được làm từ thép, nhựa, cao su…, động cơ được bố trí ở phần trước của xe
    - Nội dung của các phân tử Nước là được cấu tạo từ 2 nguyên tử hidro và 1 nguyên tử oxi, Còn hình thức là cách liên kết hoá học giữa 2 ng tử Hidro và 1 ng tử oxi
Buổi 6:
- Câu 1: Trình bày nội dung quy luật từ những thay đổi về lượng dẫn đến sự thay đổi về chất?
  - https://8910x.com/quy-luat-luong-chat/
  - Bất kỳ sự vật nào cũng là sự thống nhất giữa chất và lượng, sự thay đổi dần dần về lượng vượt quá giới hạn của độ (tức là đạt tới điểm nút) sẽ dẫn tới thay đổi căn bản về chất của sự vật thông qua bước nhảy; chất mới ra đời sẽ tác động trở lại tới sự thay đổi của lượng
  - Ví dụ:
    - Lượng -> Chất:
      - Học sinh thpt, sau khi tích đủ một lượng kiến thức, lượng thời gian 12 năm, thì sẽ biến đổi chất, trở thành sinh viên
      - Khi ta nung nóng thanh thép, nếu đạt đủ một lượng năng lượng, khiến thép tăng lên đến nhiệt độ cần thì sẽ chuyển đổi chất từ rắn sang lỏng
    - Chất -> lượng:
- Câu 2: Trình bày quy luật thống nhất và đấu tranh giữa các mặt đối lập?
  - là quy luật về nguồn gốc, động lực cơ bản, phổ biến của mọi quá trình vận động và phát triển. Theo quy luật này, nguồn gốc và động lực cơ bản, phổ biến của mọi quá trình vận động, phát triển chính là mâu thuẫn khách quan, vốn có của sự vật, hiện tượng
  - Nội dung về sự thống nhất của các mặt đối lập
    - Thứ nhất, các mặt đối lập nương tựa và làm tiền đề cho nhau tồn tại
    - Thứ hai, các mặt đối lập tác động ngang nhau, cân bằng nhau thể hiện sự đấu tranh giữa cái mới đang hình thành với cái cũ chưa mất hẳn
    - Thứ ba, giữa các mặt đối lập có sự tương đồng
  - Nội dung về sự đấu tranh giữa các mặt đối lập:
    - Sự tác động qua lại theo hướng bài trừ, phủ định lẫn nhau giữa chúng
- Câu 3: Trình bày quy luật phủ định của phủ định.
  - Quy luật phủ định của phủ định là quy luật nói lên mối liên hệ, sự kế thừa giữa cái bị phủ định và cái phủ định; do sự kế thừa đó, phủ định biện chứng không phải là sự phủ định sạch trơn, bác bỏ tất cả sự phát triển trước đó, mà là điều kiện cho sự phát triển, nó duy trì và gìn giữ nội dung tích cực của các giai đoạn trước, lặp lại một số đặc điểm cơ bản của cái xuất phát nhưng trên cơ sở mới cao hơn
  - Câu hỏi: Các Phủ Định này với Phát Triển khác nhau gì
Buổi 9:
- Câu 1: Vai trò của sản xuất vật chất?
  - Sản xuất vật chất giữ vai trò là nhân tố quyết định sự sinh tồn, phát triển xã hội của loài người,là hoạt động nền tảng làm phát sinh, phát triển những mối quan hệ xã hội
  - và trực tiếp tạo ra tư liệu sinh hoạt, tiền đề cho các hoạt động lịch sử của con người,
  - Ví dụ:
    - Con người sản xuất vật chất như gạo, thịt gia súc để cung cấp lương thực cho con người, nếu sản xuất không đạt nhu cầu thì sẽ gây thiếu lương thực, ảnh hưởng sự phát triển xã hội
- Câu 2: Lực lượng sản xuất là gì? Các yếu tố cấu thành lực lượng sản xuất? yếu tố nào quan trọng nhất vì sao?
  - Llxs là gì:
    - Lực lượng sản xuất là cụm từ dùng để chỉ tổng thể các yếu tố cấu thành nội dung vật chất, kỹ thuật, công nghệ,… của quá trình sản xuất, tạo thành năng lực thực tiễn cải biến giới tự nhiên của con người.
  - Các yếu tố cấu thành:
    - Lực lượng sản xuất bao gồm người lao động và kỹ năng lao động và tư liệu sản xuất
  - Yếu tố quan trọng nhất:
    - Con người là quan trọng nhất, vì tư liệu sản xuất phần lớn do con người tạo ra, và điều khiển bởi con người. Kĩ năng sx là cái tồn tại trong con người
- Câu 3: Quan hệ sản xuất là gì? Các yếu tố cấu thành quan hệ sản xuất? yếu tố nào quan trọng nhất? Vì sao?
  - Qhxh là gì:
    - Quan hệ sản xuất là mối quan hệ giữa con người và con người trong quá trình sản xuất vật chất. Theo nghĩa chung hơn thì quan hệ sản xuất là một yếu tố của phương thức sản xuất, là mặt xã hội của phương thức sản xuất là quan hệ kinh tế của một hình thái kinh tế – xã hội nhất định
  - Các yếu tố cấu thành: 3
    - quan hệ sở hữu đối với tư liệu sản xuất, quan hệ trong tổ chức - quản lý quá trình sản xuất và quan hệ trong phân phối kết quả của quá trình sản xuất
  - yếu tố quan trọng 1’:
- Câu 4: Mối quan hệ giữa lực lượng sản xuất và quan hệ sản xuất?
  - Lực lượng sản xuất và quan hệ sản xuất là hai mặt của phương thức sản xuất, chúng tồn tại không tách rời nhau, tác động qua lại lẫn nhau một cách biện chứng, tạo thành quy luật sự phù hợp của quan hệ sản xuất với trình độ phát triển của lực lượng sản xuất – quy luật cơ bản nhất của sự vận động, phát triển xã hội.
  - https://luathoangphi.vn/moi-quan-he-bien-chung-giua-luc-luong-san-xuat-va-quan-he-san-xuat/
- Câu 5 Cơ sở hạ tầng là gì? Các yếu tố cấu thành?
  - khái niệm cơ sở hạ tầng dùng để chỉ toàn bộ những quan hệ sản xuất hợp thành cơ cấu kinh tế của một xã hội nhất định
  - bao gồm quan hệ sản xuất thống trị, quan hệ sản xuất tàn dư của xã hội cũ và quan hệ sản xuất mầm mống của xã hội tương lai
- Câu 6: Kiến trúc thượng tầng là gì? Các bộ phận cấu thành kiến trúc thượng tầng?
  - Kiến trúc thượng tầng là toàn bộ những quan điểm chính trị, pháp quyền, triết học, đạo đức, tôn giáo, nghệ thuật, v.v. cùng với những thiết chế xã hội tương ứng như nhà nước, đảng phái, giáo hội, các đoàn thể xã hội, v.v. được hình thành trên cơ sở hạ tầng nhất định
  - Cấu trúc: 2 cái
    - Hệ tư tưởng: bao gồm triết học, tôn giáo, văn học – nghệ thuật, văn hóa- đạo đức…
    - Các thiết chế tương ứng: bao gồm nhà nước, pháp luật, các tổ chức đoàn thể, đảng phái, các cơ quan bảo vệ pháp luật nhà nước
- Câu 7 mối quan hệ giữa cơ sở hạ tầng và kiến trúc thượng tầng?
Buổi 10:
- Câu 1: Khái niêm và kết cấu tồn tại xã hội?
  - KN: Tồn tại xã hội là khái niệm triết học dùng để chỉ toàn bộ những sinh hoạt vật chất và những điều kiện sinh hoạt vật chất của xã hội trong những giai đoạn lịch sử nhất định
  - Yếu tố cơ bản: 3 yếu tố
    - Phương thức sx vật chất
    - Điều kiện tự nhiên, hoàn cảnh địa lí
    - Yếu tố về dân cư
  - SRC: https://luathoangphi.vn/vi-du-ve-ton-tai-xa-hoi-va-y-thuc-xa-hoi/
- Câu 2: Khái niệm và kết cấu của ý thức xã hội
  - KN: Ý thức xã hội là mặt tinh thần của đời sống xã hội, bao gồm toàn bộ những quan điểm, tư tưởng cùng những tình cảm, tâm trạng,… của những cộng đồng xã hội, nảy sinh từ tồn tại xã hội và phản ánh tồn tại xã hội trong những giai đoạn phát triển nhất định.
  - Kết cấu của ý thức xã hội: có 2 ý
    - Tâm lí xã hội
    - Hệ tư tưởng xã hội
  - SRC: giống câu 1
- Câu 3: Vai trò của tồn tại xã hội đối với ý thức xã hội?
  - ttxh là cái có trước ý thức xã hội đến sau vì ý thức xã hội phản ánh cái lôgíc khách quan của tồn tại xã hội.
  - Tồn tại xã hội thay đổi là điều kiện quyết định để ý thức xã hội thay đổi
  - src: https://luatthienminh.com.vn/913-giua-ton-tai-xa-hoi-va-y-thuc-xa-hoi-co-moi-quan-he-gi.html
- Câu 4: Tính độc lập tương đối của ý thức xã hội?
  - Ý thức xã hội thường lạc hậu so với tồn tại xã hội do không phản ánh kịp những thay đổi của tồn tại xã hội
  - Ý thức xã hội có thể vượt trước tồn tại xã hội
  - Ý thức xã hội có tính kế thừa
  - src: giống câu 3

Formula

CÔNG THỨC ĐẠO HÀM

CÔNG THỨC NGUYÊN HÀM

uni

How to study better Previous

What Is The Purpose Of Life Next

Notes for uni lectures

Phương pháp tính

C.trúc dữ liệu

Toán rời rạc

C.trúc máy tính và VXL

Vật lý 1

Chương 6 Điện trường:

Chương 9 Từ trường:

Chương 10 Cảm ứng điện từ:

Phương pháp tính

C.trúc dữ liệu

Toán rời rạc

C.trúc máy tính và VXL

Câu 1: Biến đổi - cộng hexa

Câu 2:

Câu 3:

Câu 4:

Vật lý 1

Phương pháp tính

Chương 2: Tổng hợp kiến thức sai số:

Chương 3: Tính giá trị hàm:

Chương 4: Giải gần đúng phương trình:

C.trúc dữ liệu

Toán rời rạc

C.trúc máy tính và VXL

Chương Input - Output

Chương Processor Structure & Function

Giải ngố định nghĩa

Vật lý 1

Dùng Chung:

1. (2đ) chứng minh hệ vector là cơ sở của R^3, tọa độ đ/v cơ sở, vector con, cơ sở, số chiều

2. (3đ) Ker, Im, cơ sở, số chiều

3. (3đ) Chéo hóa ma trận, trị riêng, vector riêng

4. (2đ) Dạng toàn phương

1. Tính tích phân suy rộng

2. Xét sự hội tụ/phân kì của tpsr

3. Đạo hàm hàm nhiều biến, gồm : hàm (riêng/ẩn/hợp)

4. giá trị lớn/nhỏ nhất hàm 2 biến trên miền bị chặn. Tìm Cực trị?

5. Vẽ các mặt bậc 2 (mặt nón elliptic paraboloid,…),Phương trình tiếp diện, pháp tuyến tại điểm

Conclusion of Linear Alg

Khi nhân các ma trận

Các mẹo làm bài

Procedure to solve determinant 4x4

Ways to find matrix rank

Ways to find reverse of matrixs

Conclusion of Math analysis

Các mẹo làm bài

Hàm số ngược

Bài tập về liên tục, gián đoạn

PP giải Maclaurin

PP giải lebnitz

Khả vi

Methods to solve lim exs

Linear Algebra

Mathematical analysis

Cực trị có điều kiện

Marxist philosophy

yếu tố quan trọng 1’: